What is a Mathematical Formula?
A formula is the way to solve or execute a difficult situation or problem. In math, a formula is an expression that through operations such as addition, subtraction, multiplication and division different quantities or variables are related.
Mathematical formulas are not just used in mathematics, but are also applied in other subject areas, such as physics, chemistry, engineering, economics, statistics, and computer science. In physics, Newton’s laws of motion are expressed by mathematical formulas, for example F = m x a (force equals mass times acceleration); in economics, the law of supply and demand can be expressed by a formula that relates the price of an item to the quantity demanded and supplied.
Elements that Make Up Mathematical Formulas
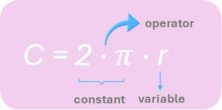
- Variables, referred to as unknowns, represent a quantity that is not known.
- Constants are numerical values that stay the same.
- Operators are the symbols that represent operations, such as addition (+), subtraction (-), multiplication (x), division (÷) and equality (=).
For example, in the formula L= 2 – π – r, L (length of the circumference) is the value to be calculated, 2 and Π are constants, the operation is multiplication and r (the radius of the circumference) is a variable.
Something very interesting about mathematical formulas is that they behave as relations. In the previous expression, if we know the value of L, the value of r can be calculated. To do this, isolate r following the rules of the equations: r = L / (2π).
In mathematical formulas, there can also be other elements such as: void (ø), integral (ʃ), and summation (Ʃ).
Types of Formulas
- Algebraic formulas- combine letters and numbers, that are linked by mathematical operations. Algebraic expressions are used to describe mathematical situations and relationships in general terms. That is, in situations where not all values are known. They allow us to express formulas, equations and mathematical models in abstract ways, which facilitates analysis and problem solving.
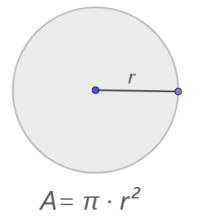
- Geometric formulas- express relationships between the measures of geometric figures. For example, the area of a circle or the volume of a prism.
Example: A= π – r²
- Trigonometric formulas- finds the mathematical relationship between trigonometric functions such as sine, cosine, tangent, cotangent, secant and cosecant. These formulas are used to solve a variety of problems in mathematics, physics, engineering and other disciplines.
- Differential and integral calculus formulas- calculate derivatives and integrals.
These are just a few examples of the many formulas that exist. There are many other techniques and specific formulas to solve more advanced problems.
Throughout history, great changes have been brought on by mathematical equations. Mathematical formulas are powerful tools that allow us to understand, model and solve a wide range of problems in various disciplines. Whether we are calculating the trajectory of a projectile, optimizing a supply chain or designing an algorithm, mathematical formulas are our guide in the vast universe of knowledge.
We hope you enjoyed this post, feel free to share it or suggest topics you would like to know more about. To learn more, register for Smartick, the online method for learning math and reading comprehension for children 4 to14 years old.
Learn More:
- Algebraic Expressions: What Are They? What Are They Used For?
- Algebra Problems: 3 Types of Activities in Smartick
- How to Solve Multiplication Word Problems
- Number Talks: Learn Math through Talking
- Combined Operations: How to Solve These Types of Problems
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024