In today’s post, we’ll be relating clocks to angles as we are learning how to calculate the angle that the two hands on a clock form.
An analog clock has 12 numbers, which divide the clock into 12 equal parts. These divisions indicate the hours. Each hour is divided into five subdivisions that amount to a total of 60 (12 x 5 = 60) divisions that indicate the minutes on a clock.
Let’s take a look, at the angles that are formed on a clock. We already know that a complete angle is 360º.
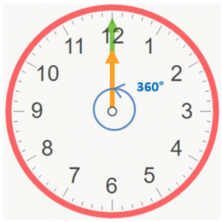
We’re going to look at the angles that the hour and minute hand run through.
The minute hand makes a complete cycle, so it goes 360º.
The hour hand moves from one number to another in an hour, and since there are 12 numbers in total, we can divide 360: 12 = 30; so, the hour hand moves 30º in one hour. Let me show you what’s going on in the table below.
Now, let’s look at how much they move in one minute. One hour is 60 minutes, so we need to divide the values above by 60.
Now, we’re going to solve the following problem.
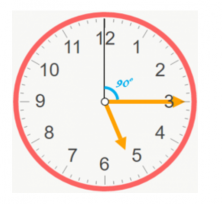
Calculate the angle that’s formed by the minute and hour hand when the clock points to 5:15.
We need to mark the angle that we want to calculate with an x:
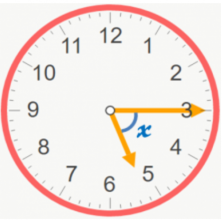
Then, we solve for the angle by starting from the last exact hour, in our example, we’ll start from 5 o’ clock sharp.
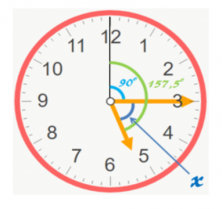
We call the distance that the hour hand travels “ang1” and the distance of the minute hand “ang2”. We’ll need this later when we calculate ang1 – ang2 = x.
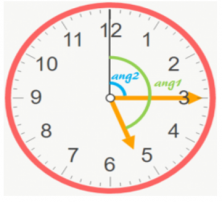
First, we’re going to separately calculate the hour hand’s distance in 5 hours and 15 minutes, and after, we’ll add the numbers together. We know that the amount traveled is one hour and a minute, so what we need to do is multiply.
In 5 hours and 15 minutes, the hour hand moves 150 + 7.5 = 157.5 degrees.
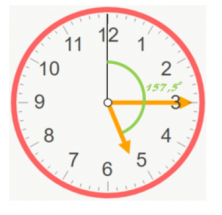
And now, we need to calculate the distance traveled by the minute hand in those 15 minutes.
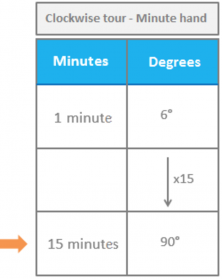
Therefore, the minute hand moved 90º.
And now, to calculate x, the only thing left to do is subtract.
157.5 – 90 = 67.5
The angle that the clock’s hands make is 67.5º.
I hope this was helpful. If you want to do more interesting problems, go to Smartick and try out our method for free!
Learn More:
- The Relationship between Clocks and Angles
- What is an Obtuse Angle?
- Basic Concepts to Help Learn How to Tell the Time
- Learn How to Measure Time and the Units Associated
- Complementary Angles: What Are They?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024