In today’s post, we’re going to look at percentages through the Singapore bar model.
To define a part of a whole, we can use a fraction, but we can also use a percentage.
The whole divides into 100 equal parts, therefore each part is 1/100 of the whole or 1%.
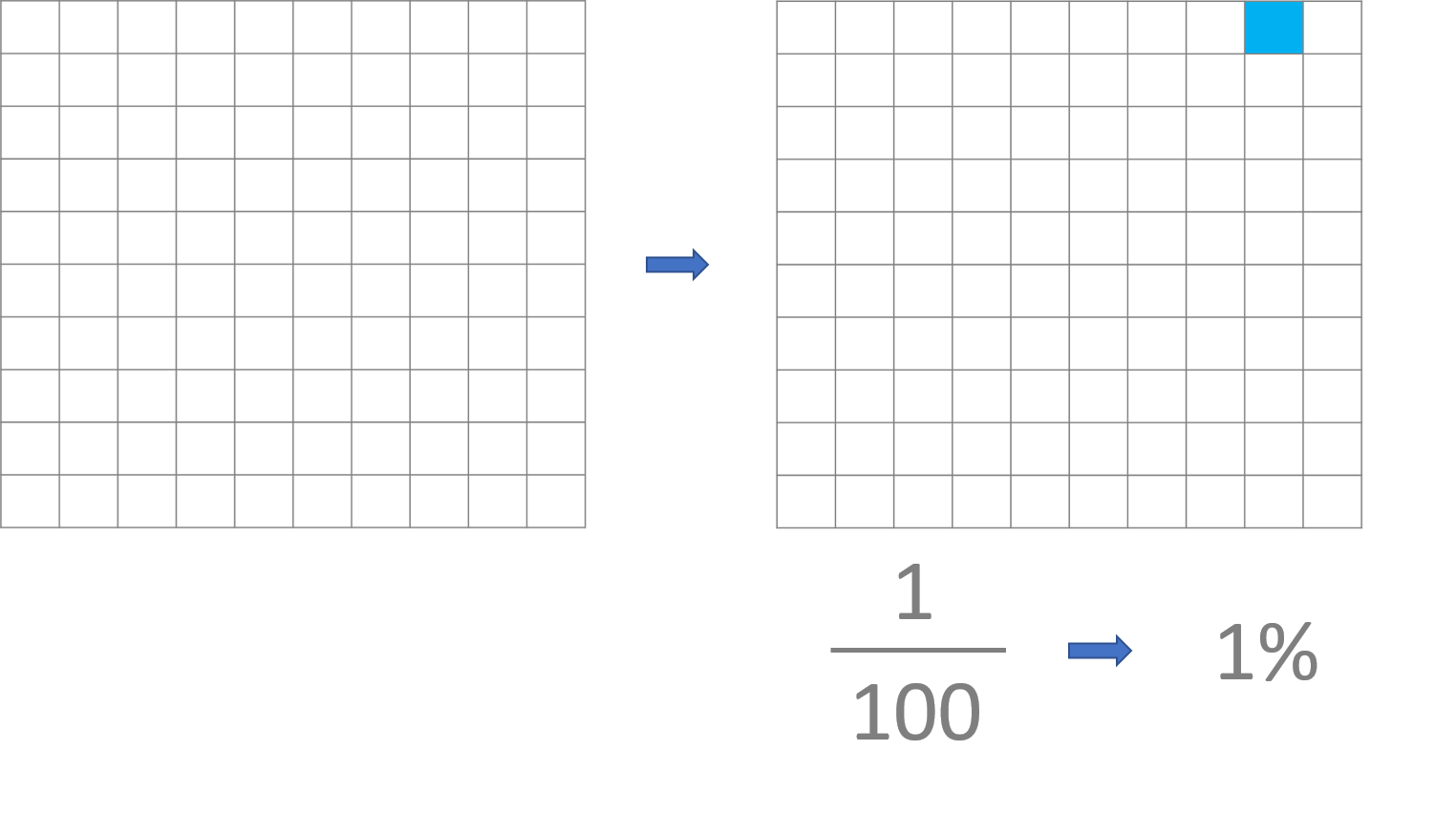
Let’s look at an example of percentages with the Singapore bar Model:
There are 400 people at a football stadium, and 60% of them are women. How many women are there in total?
In the Singapore bar model, the complete bar represents 100%, therefore the bar is 100 units. The percentage of 60% means that there are 60 units out of 100.
Let’s take a look at how we can work out 60% of 400
We know that in this case, 100 units represents 400 -> 100 units = 400
Therefore, to find out 1 unit -> 1 unit = 400/100 = 4
Now we know that 1 unit is 4 y, and we want to know what 60 units represent -> 60 x 4 = 240
60% of 400 is 240. Therefore, the number of women at the football stadium in total is 240
Now, using the same example, we’re going to see how to find the whole when we have just one part:
There are 240 women at a football stadium, which is 60% of the total number of people there. How many people are there in total?
We know that 60 units are 240 -> 60 units = 240
Therefore 1 unit is -> 240/60 = 4
We know that 1 unit is 4 and we want to know what 100 units represent-> 100 x 4 = 400
The total number of people at the football stadium is 400
Let’s look at an example of a comparison problem:
Sam has 70 euros and Tom has 30% more money than Sam. How much money does Tom have?
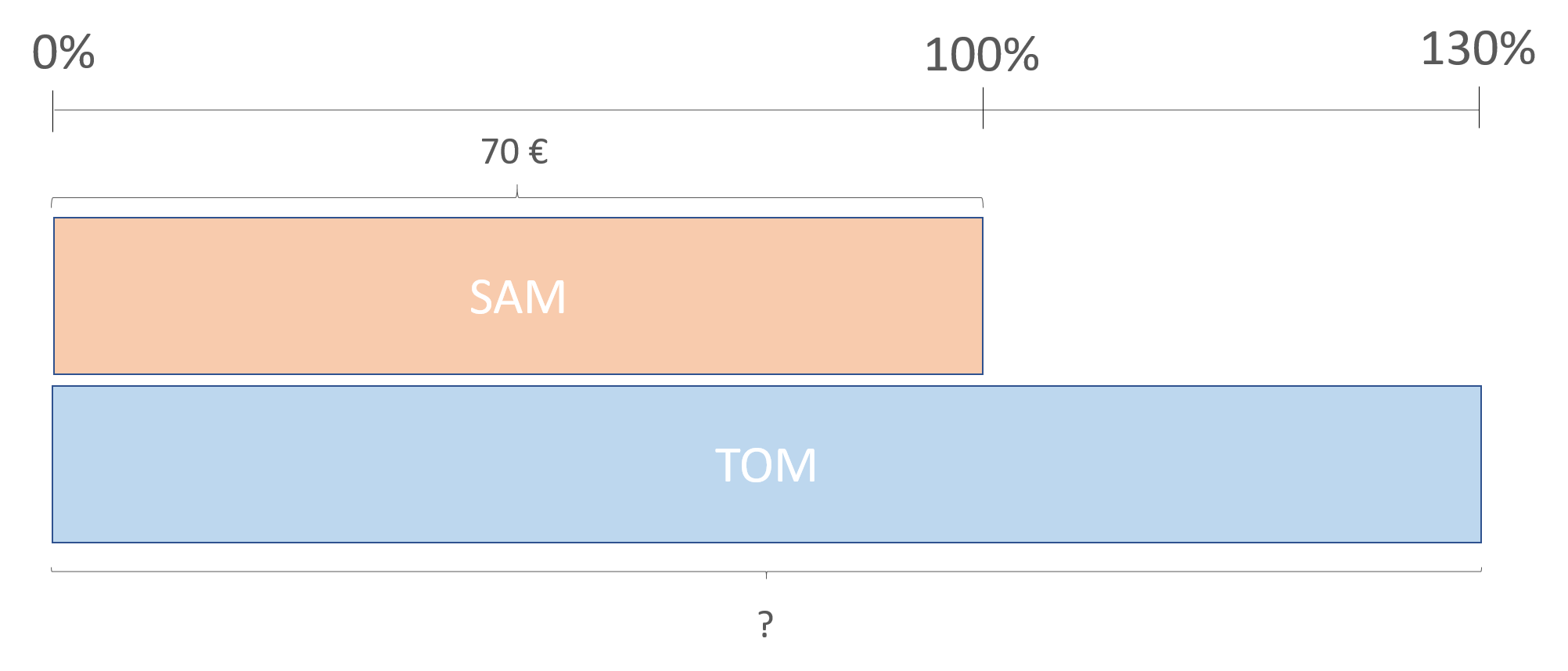
In this example, the bar representing Sam’s money acts as a base, 100%, because Tom’s money is based on the relation to the money that Sam has. In this case, Tom has 30% more money than Sam. Therefore, the amount of money Tom has is 130% of the money Sam has. The percentage 130% is 130 units out of 100, and 100 units are equivalent to the €70 that Sam has.
100 units = €70
1 unit = 70/100 = €0.70
130 units = 130 x 0.70 = €91
Therefore, Tom has €91
Let’s take a look at another example of comparison:
Julie has 50 books in her library, and Amy has 20% fewer books than Julie. How many books does Amy have in her library?
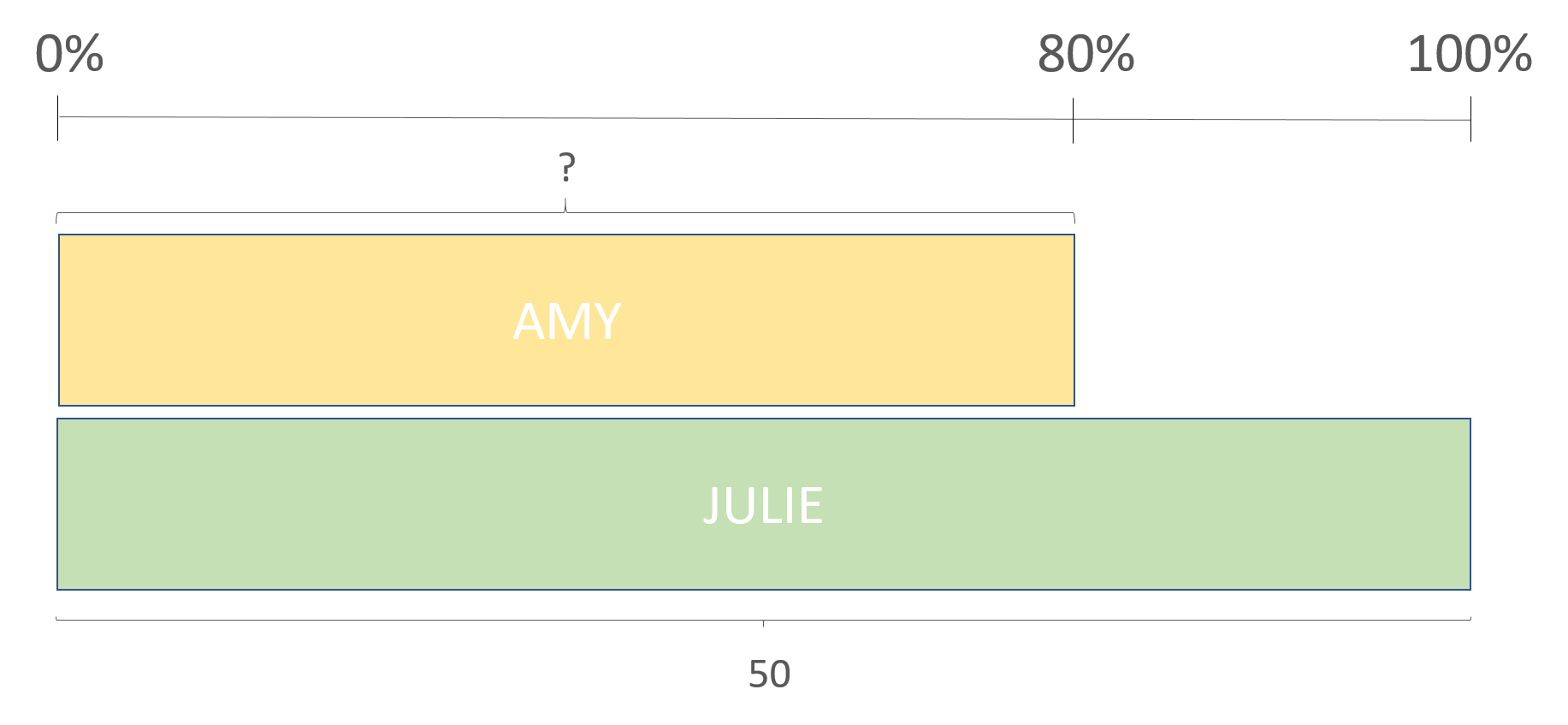
We know how many books Julie has, so we can use that amount as a base. Therefore, 50 books are 100%. Amy has 20% fewer books than Julie, therefore, Amy has 80% of the books that Julie has.
100 units = 50 books
1 unit = 50/100 = 0.5
80 units = 80 x 0.5 = 40
Amy has 40 books in her library
I hope you’ve enjoyed learning about the concept of percentages and how to solve them. If you want to keep practicing, log in to Smartick.
Learn More:
- Using Singapore Bars to Help Solve Problems II
- Rule of Three for Calculating Percentages
- Using Singapore Bars to Solve Algebraic Equations
- Let’s Learn about Ratios with Singaporean Bar Models
- Singapore Bars Applied to Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.