Today we’re going to learn how to perform a division of fractions using the very definition of division as the inverse operation of multiplication. This way we don’t need to use the more known methods that we’ve already seen in the post about Dividing fractions.
You might know how to use those methods, but without knowing what they mean. Learning how to divide fractions this way will give you a deeper mathematical understanding of the operation.
Example of division of fractions
Let’s take a look at how to solve the following division using mathematical compression:
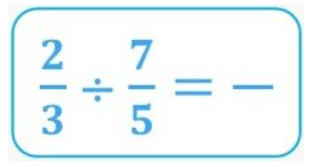
Since division is the inverse operation to multiplication, we have to find a fraction that, when multiplied by 7/5 gives us a result of 2/3. Let’s see how to find it, I’m sure it’ll be easy for you.
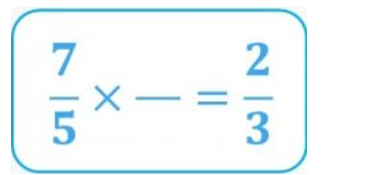
Steps to find the result of the division
Making use of the simplification of fractions, let’s see how we can find the unknown term of our product, step by step.
- Since we have a 7 as the numerator of the first term of the product and we don’t want it to appear in the result (which we already know is 2/3), if we put it in the denominator of the fraction that we’re multiplying by, it will disappear through simplification:
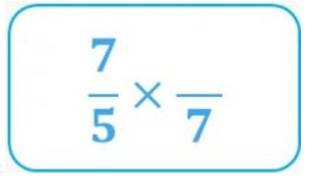
- Since we have a 5 as the denominator and we don’t want it to appear in the result (which we already know it is 2/3), if we put it in the denominator of the fraction that we’re multiplying by, it will also disappear through simplification:
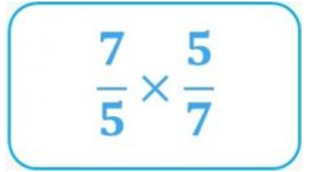
- Now we need a 2 for the numerator, so we multiply this numerator by 2:
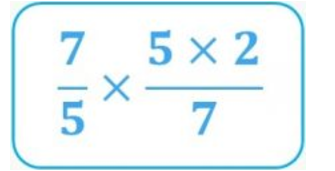
- And finally, since we want a divisor of 3, we multiply this denominator by 3:
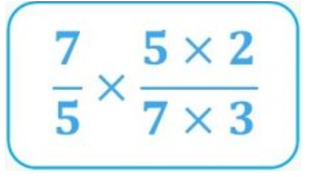
Result of the division
We’ve found the fraction we were looking for! So:
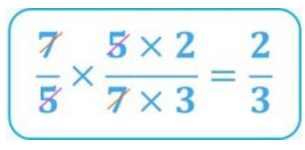
By doing the operations we get the fraction 10/21:
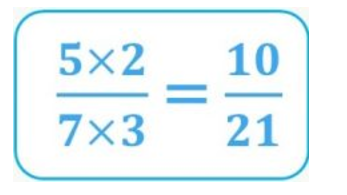
Therefore, since:
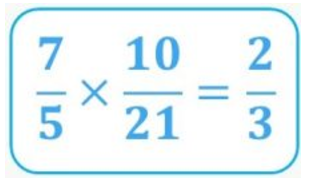
Then:
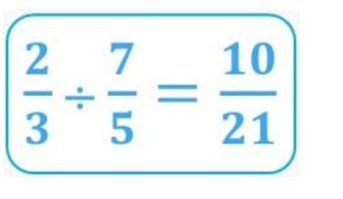
See how easy it is when you use simplification? And more importantly, when you understand mathematically what we’re doing.
If you found this post useful, you can read more about fractions on our blog. Some related posts are:
- Word Problems with Division of Fractions
- Learn How to Divide Fractions with Two Different Methods
And if you want to learn more about mathematics, register with Smartick and try it for free.
Learn More:
- Two Ways of Dividing Fractions and Some Examples
- Review and Practice the Two Methods of Dividing Fractions
- Learn New Methods for Dividing Fractions
- Learn How to Divide Fractions with Two Different Methods
- Learning How to Subtract Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024