Do you know what a cylinder is? In addition to explaining what cylinders are, in this post we will look at how they develop, the parts that make up a cylinder, and how to calculate its area and volume. We will also show you some activities using cylinders that children complete during their Smartick sessions.
Index
What is a Cylinder?
A cylinder is a geometric body that is formed by a rectangle that rotates around one side. In mathematics, it is also defined as the cylindrical surface that is formed when a parallel line rotates around another parallel line, which we call an axis.
To clarify this concept, we should keep in mind that we are talking about a solid cylinder, that is, a geometric body. We call the surface of a cylinder a hollow cylinder. Here’s an example:
The calculations that we are going to do in this post are for solid cylinders.
Types of Cylinders
There are two types of cylinders:
Rectangular Cylinder
When the axis of the cylinder is perpendicular to the base.
Oblique Cylinder
If the axis is not perpendicular to the base.
How Do You Draw the Surface Development of a Cylinder?
The development of a geometric body is to see its entire surface on a plane, in this case, the surface of a solid cylinder. But be careful! You need to make sure that it has bases because, for example, if you “develop” a roll of toilet paper you will only have a rectangle.
The development of a cylinder consists of a rectangle, which is the lateral part of a cylinder, and two circles which are the bases. If you would like, you can read this post on geometric figures to remember the principal characteristics of rectangles and circles.
What Characteristics do Cylinders have?
When we create a cylinder by rotating a rectangle:
- The axis is the side of a rectangle that remains fixed when turned.
- The bases are two circles, perpendicular to the axis. They are the covers that close the cylinder.
- The height is the distance between the bases.
- The radius (r) is the length from the axis to the extreme of the cylinder and corresponds to the radius of the base.
How do You Calculate the Area of a Cylinder?
You have to consider the development of a cylinder and calculate the area of its parts, the rectangle and two bases.
Area of the rectangle = 2 × π × r × h
Area of the base = π × r2 (Remember that it has two bases!)
Adding up everything gives us the area = 2 × π × r × h + 2 × π × r2
Area = 2 × π × r × ( h + r )
Example of the Area of a Cylinder
- Calculate the area of a cylinder with a radius of 3 cm and a height of 6 mm.
First, we must make sure that the radius and height are using the same type of measurements which is why we need to convert the measurement for height in millimeters to centimeters. If you would like to, you can review this post about measurements of length to refresh your memory.
60mm = 6cm
Now we are going to calculate the area of the rectangle that is equivalent to the side surface of the cylinder. As we have indicated in the formula earlier, we just substitute the values of the cylinder:
Area of the rectangle = 2 × π × r × h
2 × 3.14 × 3 × 6 = 113.04 cm²
We also need to calculate the area of the bases, which is equal to a base but times 2. We use the formula that was given to us earlier and substitute the values:
Area of the bases = 2 × π × r2
2 × 3.14 × 9 = 56.52 cm²
And finally, we add the parts of the cylinder, the lateral area, which is the area of the rectangle, and the area of the bases:
Area of the cylinder = 2 × π × r × h + 2 × π × r2
113.04 + 56.52 = 169.56 cm²
How do You Calculate the Volume of a Cylinder?
The volume is equal to the are of the base times the height, remember that we indicate the height with the letter “h”.
Volume = π × r2 × h
Example of the Volume of a Cylinder
- Calculate the volume of a cylinder with a radius of 5cm and a height of 60 mm.
As indicated above we must put both the radius and height in the same unit of measurement. We need to convert the height from millimeters to centimeters:
60mm = 6cm
In order to calculate the area of the base we multiply π by the radius squared:
Area of the base = π × r2
3.14 × 25 = 78.50 cm²
And to find the volume of a cylinder we have to multiply the area of the base by 6 cm which is the height:
78.50 × 6 = 471 cm³
To calculate this volume we have multiplied an area (squared units) by a height (linear units), so we have cubic units as a result. Remember that the unit to measure volume in the International System of Units is the cubic meter (m³), although we have used cm³, which is its submultiple.
What we have calculated applies whether the cylinder is a straight or oblique cylinder. Think about it, if it is like the coin tower which we represented as an oblique tower if we made it straight it would have the same volume.
Examples of Exercises Identifying Geometric Figures in Smartick
To continue, we are going to look at the different types of exercises that we have in Smartick to learn how to identify a cylinder.
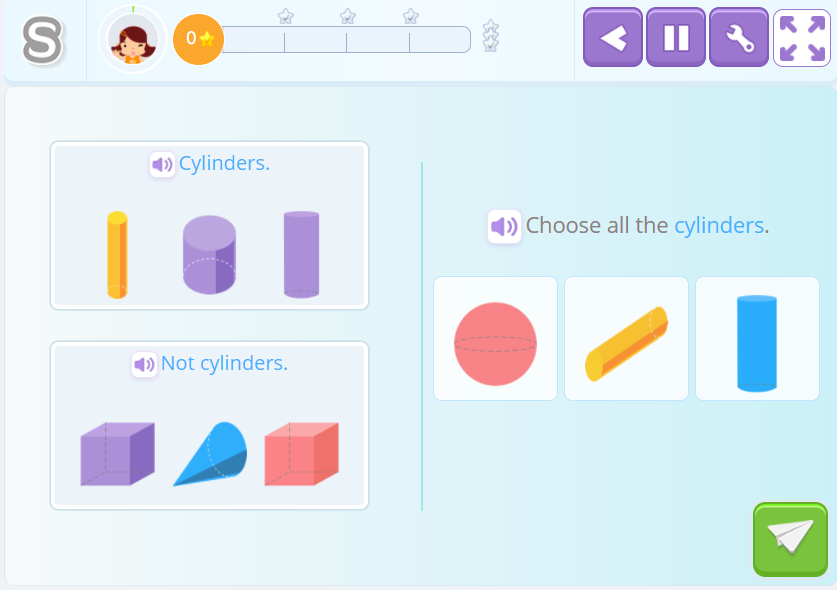
Identifying Geometric Figures
Identifying Geometric Figures in an Image
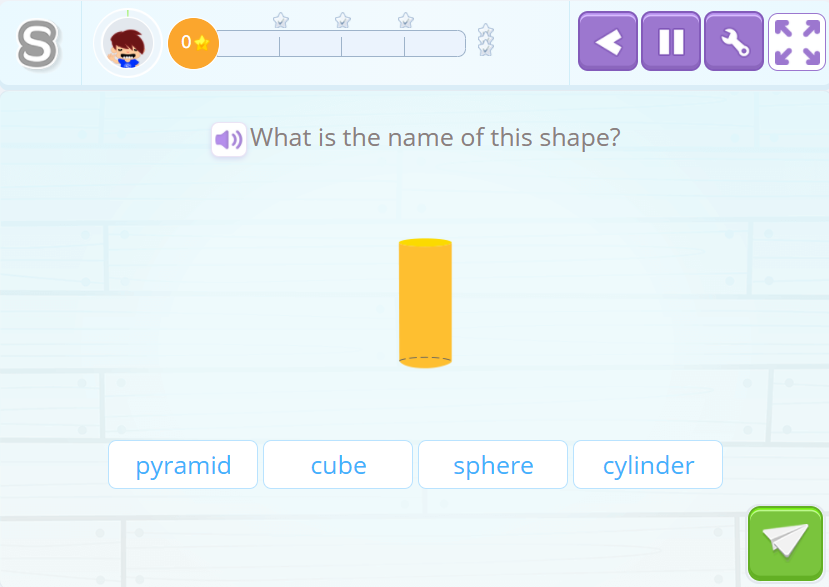
A geometric figure appears and the child should identify and select its name from the different options given.
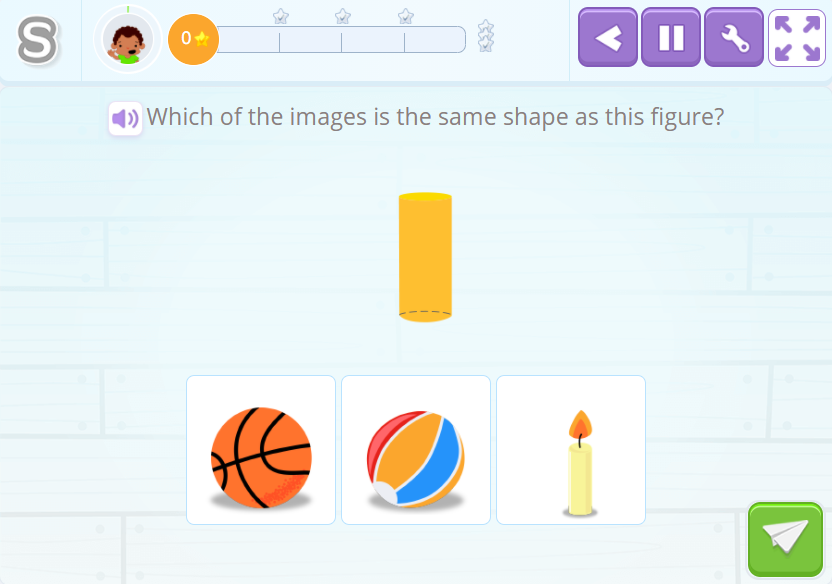
Comparing a Cylinder with Real-Life Objects
The child should identify which real-life object of those presented resembles a cylinder. As visual support, they are presented with the geometric body.
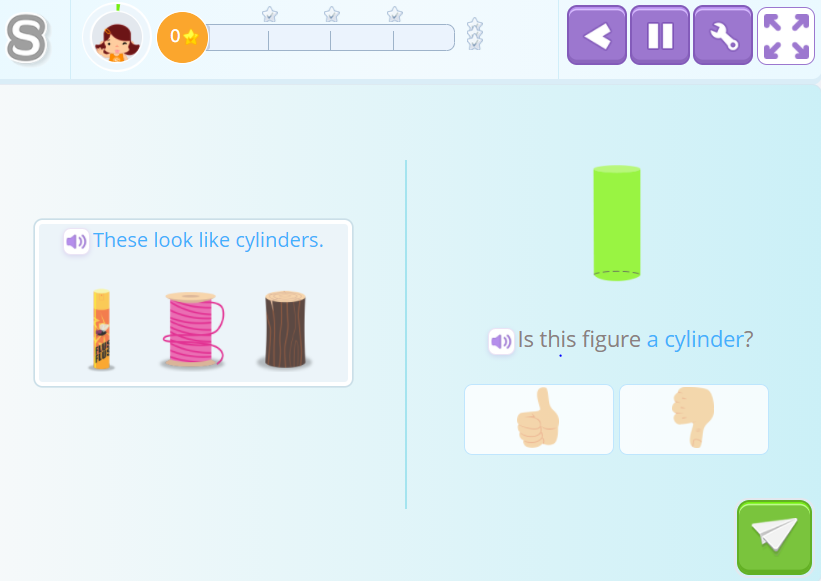
Identifying if a Real Object is Similar To a Cylinder
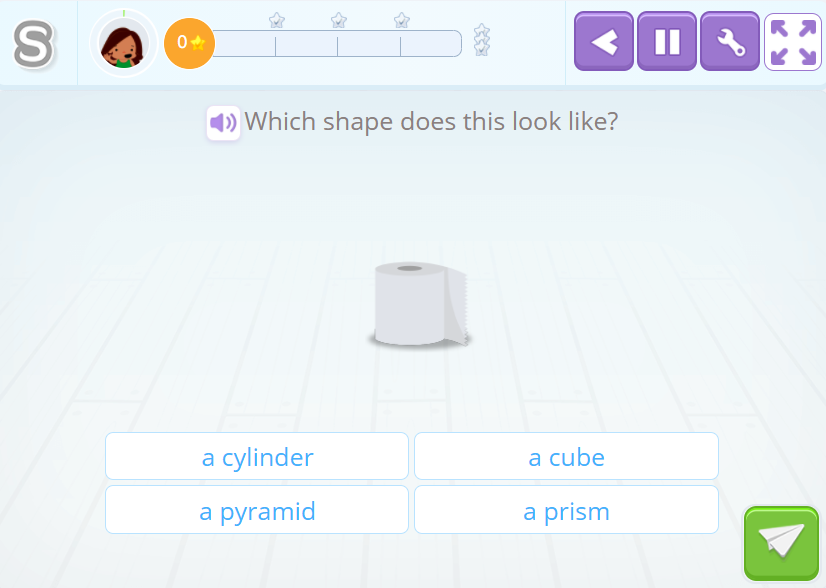
Identifying the Name of a Geometric Figure That Looks Like a Real Object
The child is presented with an object from daily life and they need to select its name among the options given.
These are just a few examples of Smartick’s activities. If you would like to learn more, register with Smartick and try our online method for free.
Learn More:
- What Is a Prism? Solve These Exercises to Find Out
- Learn the Properties of Geometrical Prisms
- What Are Solid Geometric Shapes or Bodies?
- Commutative Property in Multiplication and Addition
- Learn the Associative Property of Multiplication
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024