Today you will learn what symmetry is and we will see some symmetry exercises that children do during their Smartick sessions and the typical mistakes that are usually made.
Index
What is Symmetry?
Symmetry is one of the mathematical concepts that students start to learn about outside of school. Yet, they still study it in early childhood education and build symmetrical figures without utilizing a rigorous definition.
As we will see below, there are various types of symmetry. We are going to begin with the most well-known, symmetry with respect to a line or axial symmetry. Let’s start by drawing a straight line on a plane, which in this case it can be on a piece of grid paper like what is pictured below:
We say that a figure is symmetrical with respect to a line when each point on one side of that line has another point on the other side, and at the same distance, from that line.
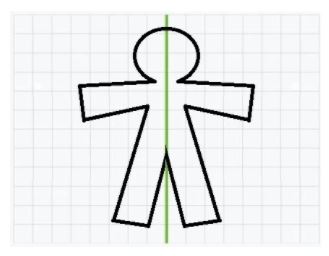
If we want to know if an image is symmetrical with respect to a line and we have it on the piece of paper, we just need to fold the paper along the line. If when we fold the paper and the figures coincide with one another it is because they are symmetrical with respect to the line. If they do not coincide then they are not symmetrical.
If we want to create a symmetrical image on the paper, we begin by folding the paper and, using a marker that will bleed through the paper slightly, we draw the figure that we want. Then we unfold the paper. The marker has bled to the other side and has created two figures that are symmetrical with respect to the line that we had folded. When the paper is folded, they match up exactly. We could also use scissors instead of a marker.
Video: Symmetrical Figures and Axes of Symmetry
To better understand what symmetry is with respect to an axis, take a look at this video of one of our interactive tutorials. It is no longer interactive but you have the advantage of being able to watch it as many times as necessary and sharing it with others. If you would like to access the real interactive tutorials, register with Smartick, the online math learning method for children ages 4 to 14.
In this video we present a symmetry workshop, take a look:
What is an Axis of Symmetry?
A symmetrical figure can have one or various axes of symmetry, that can be straight lines or lines that divide the figure into two symmetrical parts.
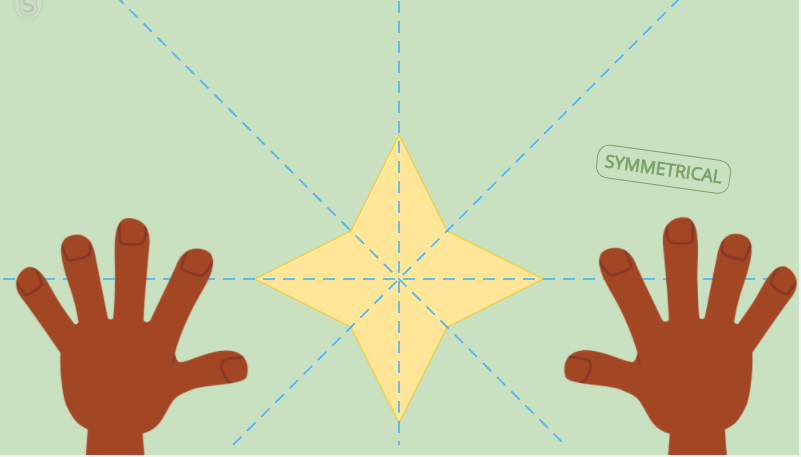
In the image, taken from the video, the star has four axes of symmetry and the hands only have one – vertical straight.
Types of Symmetry
There are many types of symmetry but we are going to focus on these three which are the ones that would be seen in school:
- First, axial symmetry, or symmetry with respect to a line, is the one that divides an object or figure in two using a straight line, in other words, by an axis of symmetry. This type of symmetry might resemble when we look in the mirror and see our reflection in it.
- We say that one or more figures have rotational symmetry when they are not altered when rotated at a certain angle. The four-pointed star in the previous image has rotational symmetry because if you turn it 90º (or any multiple of 90º) it will be the same.
- The third type of symmetry that occurs on a plane is symmetry with respect to a point or central symmetry. Two points are symmetrical with respect to a point – which we call the center of symmetry – if they are the same distance from it and on the same line. Central symmetry produces the same effect as a 180º turn.
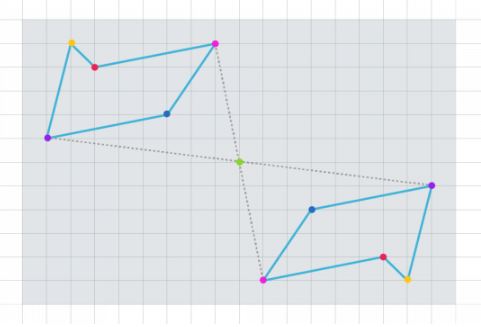
Symmetry Exercises in Smartick
In the post about new Smartick content, we gave examples of the sequence of symmetry activities. The difficulty varies with the shape of the figures and the orientation of the axis of symmetry. The difficulty gradually increases, little by little, facilitating learning and comprehension of this concept. These exercises promote the development of spatial vision and geometric reasoning.
- We have exercises where children have to analyze if two figures are symmetrical:
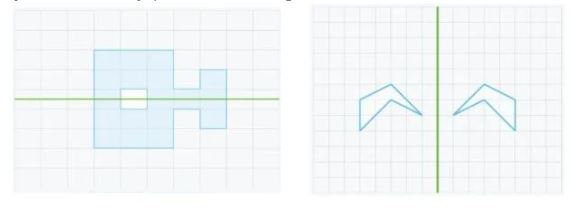
- In others they must construct symmetrical figures:
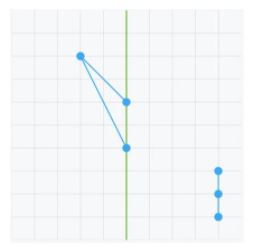
- Or place a series of points symmetrically on an oblique axis:
Typical Mistakes
Are these two figures symmetrical with respect to the axis? There are two mistakes that students often make when faced with this question.
- Think about if the figures are identical, if they are then they are symmetrical:
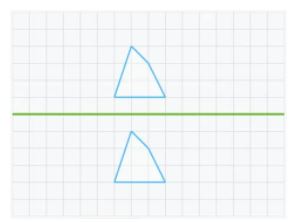
In order to correct this error, (as we mentioned earlier) it is useful to think of the grid as a paper that can be folded on the axis of symmetry. If when folded, the figures do not coincide it is because they are not symmetrical. Another way is to think of the axis as a mirror, if one figure is not the reflection of the figure that would be projected in the mirror, then they are not symmetrical.
- Another common mistake is to think that if one figure is the specular reflection of another then they are symmetrical regardless of their position with respect to the axis of symmetry:
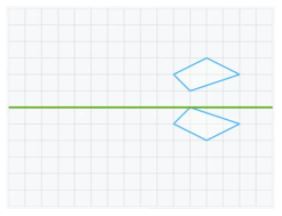
We can use the same strategies as before to eliminate this mistake. If we fold the paper along the axis of symmetry the figures do not match. And one figure is not the reflection of the other in the axis mirror. Therefore, these two figures are not symmetrical with respect to the axis.
Symmetry Outside of Mathematics
Symmetry is all around us:
- In a mirror or the reflection on the water’s surface. The image reflected is symmetrical to the real image.
- In ourselves: we have a right hand and a left hand, a right ear, and a left ear, and each pair is symmetrical. Our body is divided into two symmetrical parts, right and left, with respect to an axis that runs from the top of our heads to our toes.
- The majority of houses and buildings have facades that are symmetrical with respect to a vertical axis.
- Cars, toasters, cell phones, a glass, a plate, a bottle, a television, a sofa… most daily objects have one or more axes of symmetry.
- We can also find symmetry in art. Artists use symmetry in painting, sculpture, music, and countless other disciplines.
- In nature too. The majority of animals and plants have some type of symmetry: bilateral, radial…
If you would like to learn more about primary school geometry and mathematics, register with Smartick and try it for free.
Learn More:
- Identifying Flat Symmetrical Figures
- Trapezium-Trapezoid: Definition, Types and Exercises
- Mathematical Functions: Do You Know What They Are?
- Geometric Figures and Straight Lines
- Elementary Geometry – Open Lines
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024