What is a set? What types of sets are there? How can you relate one to another? How do they help me? We’ll explain them here.
Index
What is a set?
A set is a collection of items with some common characteristic which we use to define them by and treat it as an item.
Here are some examples:
- First with real items:

The items in the circle form a set based on a common attribute (something that is true about all of the items).
All of these items have different characteristics, but what they have in common is that they are all animals. Thus, we can call this the set of ANIMALS. Of course, there would be more items than those shown in the circle in this set!
- Now with numbers:
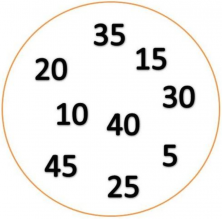
All these numbers have different characteristics, but what they have in common is that they are all multiples of 5. Thus, you can call this set of MULTIPLES OF 5. Of course, there would be more items than those shown in the circle in this set! (Infinite items in this case!)
Relationship Between Several Sets
Independent
Are sets that are not related to each other. They may have some of the same items, but this is simply a coincidence.
Let’s look at some examples:
- First with real items:

Two independent sets that consist of one designated for animals and another for transportation.
One circle represents the set of animals and the other circle represents the set of means of transportation. They do not have any relationship, so they are said to be independent sets.
- Now with numbers:
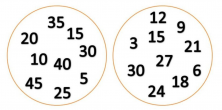
Two independent sets that consist of one designated for multiples of 5 and another for multiples of 3.
One circle represents the set of multiples of 5 and the other circle represents the set of multiples of 3. They do not have any relationship, so they are said to be independent sets.
Notice that they do have some items in common (multiples of 15), but that is a coincidence because the basis on which the individual sets are formed are not related.
Inclusion & Subsets
When we look at the characteristics in a group and find that some items have additional common features, we are considering subsets, in other words, a set belonging to another set.
Let’s look at some examples:
- First with real items:

Group of animals in which there is an additional separation, those that can fly.
Within the group of animals, we have identified those that can also fly. We can call this subset the FLYING ANIMALS Subset.
- Now with numbers:
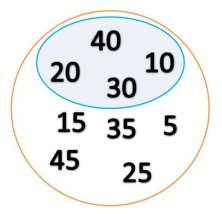
Inside the set of multiples of 5, there is the set of multiples of 10. And we see that all multiples of 10 are multiples of 5, that is to say, the MULTIPLES OF 10 Set is a subset of the MULTIPLES OF 5 set.
Intersection
The intersection is the “overlap” of two (or more) sets—that is, the set of items that belong to both sets.
Let’s see some examples:
- First with real items:

In one circle is the set of ANIMALS, while the other circle represents things that TRAVEL BY AIR.
Within the TRAVELS BY AIR set, there are some items that have features in common with some items of the ANIMALS set. These items form the intersection of the two sets.
- Now with numbers:
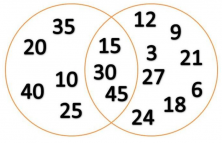
Two overlapping circles representing the sets of multiples of 5 and the multiples of 3. In the section of the common space between the two circles are numbers that are multiples of both.
By observing the MULTIPLES of 5 set and MULTIPLES of 3 set, we see that we have items that are multiples of 5 and 3. These items form the intersection of the two sets.
Union
The union of two sets is the set that includes all items of both sets. So we say that its items have the characteristics of one or the other set.
Let’s see some examples:
- First with real items.

The union of the sets of ANIMALS and TRANSPORTATION METHODS groups those items that are animals or means of transport.
- Now with numbers:
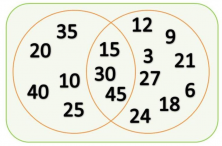
The union of the MULTIPLES of 5 and MULTIPLES OF 3 sets encompasses those items that are multiples of 5 or 3. Not like the intersection, which includes only those that are multiples of 5 and 3.
The work in the classroom with sets and Venn diagrams develops not only mathematical-logical intelligence but the ability to classify and manage reality according to their characteristics. This helps children to build their own conceptual network and, thus, learn.
Check out more posts about Venn Diagrams below:
If you enjoyed this post and want to keep learning, you can try Smartick’s free trial!
Learn More:
- Introduction to Sets and Subsets
- Manipulative Games to Practice Set Theory
- Venn Diagrams, Set Diagrams and Logic Diagrams
- Learn about Set Theory and Study Techniques
- Classification: First Steps towards Logical-Mathematical Thinking








You’ve got a typo. Under the heading INTERSECTION, at one point your refer to “Travels by Water” when you mean “Travels by Air.”
Thanks for your comment, corrected!
Liked the way the content is presented.