Dec11

Measurements of Time: Biennium, Lustrum, Decade, Century, Millenium

13 Comments

In this post we’re going to look at measurements of time that refer to quantities of years: biennium, lustrum, decade, century, millenium

If you want to review previous posts on units of time, you can do so here:

Before you read on, the most important thing you need to understand is the following:

century

We’re going to practice these concepts using a few problems that you can find during your daily Smartick sessions. Let’s start!

Problem 1

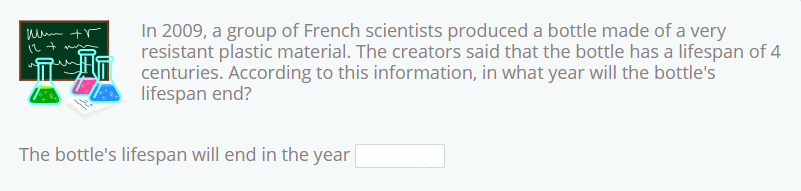
century

To solve this problem, we have to remember that a century is 100 years, therefore 4 centuries are 4×100=400 years.

Knowing this, we just have to add these 400 years to the year in which the bottle was made, 2009.

Therefore 2009 + 400 = 2409

Answer: The bottle’s lifespan will end in 2409

Problem 2

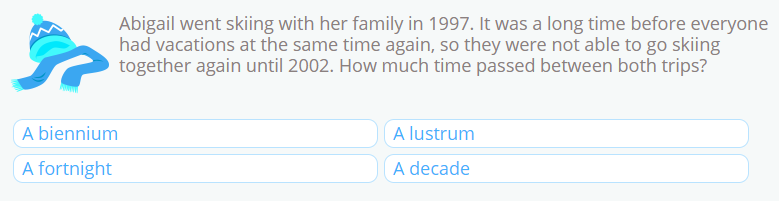
century

To solve this problem, we need to subtract the dates.

2002 – 1997 = 5

The unit of time equivalent to 5 years is a lustrum.

Answer: A lustrum passed between both trips

Problem 3

century

The first thing we need to do to solve this problem is calculate the number of years that pass between 3655 B.C. and 2010.

To do this, we add 3655 and 2010. 3655 + 2010 = 5665

Now we need to break this length of time down into smaller units.

5000 years is 5 millennia

600 years is 6 centuries

60 years is 6 decades

5 years is a lustrum

Therefore, 5 millennia + 6 centuries + 6 decades + one lustrum

Answer: 5 millennia, 6 centuries, 6 decades and one lustrum had passed

Problem 4

century

To solve this problem, first we need to take into account that the rock is now ¹/₄ of its original size, which means that it has lost ³/₄ of its size.

If 13 lustra pass for every quarter, we need to multiply this amount by 3. 3 x 13 = 39 lustra

Now we just need to multiply the 39 lustra by the 5 years that each lustrum contains:

39 x 5 = 195

Answer: It has been exposed to 195 years of erosion

I hope these exercises have helped you understand larger units of time. Remember, if you want to practice more of these problems and many others like how to calculate lcm, register with Smartick and do your session every day.

Learn More:

Fun is our brain’s favorite way of learning

Diane Ackerman

Smartick is a fun way to learn math

15 fun minutes a day
Adapts to your child’s level
Millions of students since 2009

Author
Recent Posts

Smartick

Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.