We’ve already written various posts about dividing by 3 digits:
- Learn How to Divide with 3-Digit Numbers
- Practice 3-Digit Division Examples
- Learn How to Do a 3-Digit Division Problem
Today we’re going to look at another, more complicated, example. Let’s start and divide by 3 digit numbers!
1. How many digits are there in the divisor? 3!
2. We take the same number of digits in the dividend
3. We compare the 3 digits in the dividend with the 3 digits in the divisor.
Since 385 is greater than 125 we can start dividing.
4. We divide the first digits of the dividend and the divisor.
3 divided by 1 is 3. We need to multiply 125 by 3 and see if it goes into 385.
125 x 3= 375.
We get 375 so we know it fits. We put the 3 in the quotient.
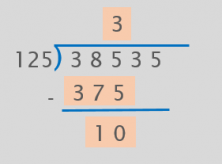
5. We bring down the next digit of the dividend.
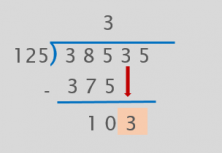
We’ve brought down the 3 but now 125 doesn’t go into 103. So, how can we continue?
When this happens, we have to add a 0 to the quotient and bring down the next number in the dividend.
Now we can keep dividing.
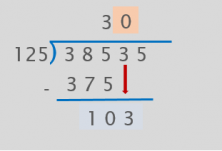
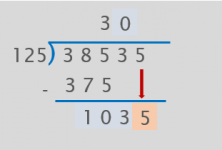First we divide 12 by 1 to see what number to put in the quotient. 12 divided by 1 is 12, and since it is greater than 10, we keep 9, the greatest one-digit number.
125 x 9 = 1125.
And 1125 doesn’t go into 1035.
Let’s try it with the next smallest number, 8.
125 x 8 = 1000.
That’s it!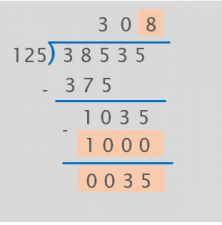
We’ve finished the division.
38,535 divided by 125 gives us a quotient of 308 with a remainder of 35.
The only thing left to do, as always, is to check our work:
divisor x quotient + remainder = dividend
125 x 308+ 35 = 38,535
It works!
Now we know how to divide by 3 digits. If you want to keep learning more primary mathematics, register with Smartick and try it for free.
Learn More:
- Learn How to Divide with 3-Digit Numbers
- Practice 3-Digit Division Examples
- Learn How to Do a 3-Digit Division Problem
- Learn to Divide by One Digit with an Example
- How to Solve a Problem Involving Dividing 2 Digit Numbers
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024