Are you ready to learn how the greatest common factor is calculated? We’ll explain it to you in this post along with examples and videos to help you better understand the GCF. It’s also called GCD (Greatest Common Divisor) and HCF (Highest Common Factor). Let’s go!
Index
What is the Greatest Common Factor (GCF)?
In mathematics, the largest number that divides into two given numbers exactly is called the greatest common factor or GCF. As we talk about the largest number we will only be taking positive numbers into account.
We also can say that the greatest common divisor of two numbers, “A” and “B”, is the largest number that divides into the two numbers, both A and B.
For example, we will say that the greatest common divisor of 18 and 24 is 6 because 6 is the largest of the common divisors (or factors) of 18 and 24. We write it as GCD (18, 24) = 6.
Numbers where the divisions result in a remainder of zero are taken into account. If you would like, you can review dividing by one digit to refresh your memory about the different components of a division problem.
Video: Greatest Common Factor
To better understand the greatest common factor of two numbers, take a look at the following video.
It is a video of one of our interactive tutorials and although it is not interactive in this format, you are able to watch it as many times as necessary and share it with friends. If you would like to access our interactive tutorials, register with Smartick! The online method which helps children ages 4 to 14 learn and practice personalized math.
What is the Greatest Common Divisor used for?
GCF to Simplify Fractions
One use for the greatest common divisor is to simplify fractions.
For example, to simplify the fraction 12/18, first calculate the Greatest Common Divisor of 12 and 18, which is 6.
Then, we have to divide the numerator and denominator of the initial fraction by 6 in order to obtain the simplified fraction, 2/3.
GCF to Calculate the Least Common Multiple (LCM)
The greatest common divisor can also be used to calculate the least common multiple of two numbers, their LCM.
This is because the product of the greatest common divisor and the least common multiple of two numbers is equal to the product of those two numbers.
Let’s look at this with an example. As we have said before, the GCF of 12 and 18 is 6, and since 12 x 18 = 36, their least common multiple must be 36 because 3 x 36 = 216.
GCF to Solve Problems
Without a doubt, you are going to use the GCF to solve most problems.
Terms
Now, we are going to explain some of the concepts used to calculate the GCF for various numbers. It is important to learn them so that we are familiar with them and can recall them while problem-solving.
Divisor
The divisor of a number is the value that divides the number into two exact parts and therefore having a remainder of zero.
Let’s look at an example of this:
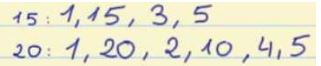
First, we calculate the divisors of 15:
- 15 / 1 = 15, therefore 1 and 15 are divisors of 15.
- 15 / 2 = 7, the remainder is 1, so 2 is not a divisor of 15.
- 15 / 3 = 5, therefore 3 and 5 are divisors of 15.
- 15 / 4 = 3, the remainder is 3, so 4 is not a divisor of 15.
Now we should divide by 5, but since we already have it as a divisor we have finished calculating the divisors for 15.
Therefore, the divisors of 15 are 1, 3, 5, and 15.
We can also calculate the divisors of 20:
- 20 / 1 = 20, therefore 1 and 20 are divisors of 20.
- 20 / 2 = 10, therefore 2 and 10 are divisors of 20.
- 20 / 3 = 6, the remainder is 2, therefore 3 is not a divisor of 20.
- 20 / 4 = 5, therefore 4 and 5 are divisors of 20.
Now we should divide by 5, but since we already have it as a divisor we have finished calculating the divisors for 20.
In other words, the divisors of 20 are 1, 2, 4, 5, 10, and 20.
Common Divisor
it is a number that is a divisor of two or more numbers. IN other words, a common divisor among those numbers.
If we continue with the previous example where we calculated the divisors for numbers 15 and 20, now we can take a look at what their common divisors are.
Divisors of 15: 1, 3, 5, and 15.
Divisors of 20: 1, 2, 4, 5, 10, and 20.
What common divisors do 15 and 20 have?
In this case, if you look closely, the common divisors for 15 and 20 are 1 and 5.
Greatest Common Divisor
As we saw at the beginning of the post, the greatest common divisor is the largest of the common divisors.
let’s see what the greatest common divisor is from the previous example, the GCF (15, 20).
Divisors of 15: 1, 3, 5, and 15.
Divisors of 20: 1, 2, 4, 5, 10, and 20.
Now you know the common divisors of 15 and 20 are 1 and 5. Now, between these two numbers (1 and 5) you need to choose the larger number, which is 5. Therefore, the greatest common divisor of 15 and 20 is 5.
How to Calculate the Greatest Common Factor
There are several methods to find out the greatest common divisor of a number. We are going to look at two.
Method 1 to Calculate GCF
This is the method that we have been using in the examples above. For this method, it is very important to look at what greatest common divisor means.
- We write out all of the divisors for each number and from these, we pick out the common divisors.
- The largest divisor will be the GCF of these numbers.
A drawback of this method is that a large number can have many divisors and writing them all out can be time-consuming. The advantage, however, if you have taken it into account, is that sometimes you do not need to calculate anything. For example, if you are asked for the greatest common divisor of three numbers and it turns out that one of the numbers divides into the others, you already have the greatest common divisor. The greatest common divisor for numbers 36, 12, and 84 is 12 because it can be divided into the other numbers and there is no other common divisor larger than 12 that can do that.
Method 2 to Calculate GCF
Decomposing, or breaking down, numbers into factors or prime numbers.
- Decomposing each number into prime numbers.
- Next, we find the common factors.
- Then, we choose the factor with the least exponent from the common factors.
- And finally, we multiply the chosen factors.
Let’s look at an example:
We calculate the GCF of 8 and 12.
As you can see, we have chosen the common factors, in this case 2, but you need to be careful and look closely at the smaller exponent (2²), which is equal to 4. If you would like more practice you can refresh your memory about how to decompose factorials and exponents.
Video to learn how to calculate the GCF by decomposition of factors
In the following video, you can see how Eva and Leo use the greatest common divisor to help families from their school who need school materials and books.
This is a video of one of our interactive tutorials. If you would like to access our interactive tutorials and solve them yourself, register with Smartick! The online method which helps children ages 4 to 14 learn and practice math with daily sessions adapted to their unique level and rhythm.
GCF Examples and Exercises
We are going to see a few examples of the exercises that use the methods that were just explained. Method 1, looking for divisors, and method 2, decomposing numbers into factors to calculate the greatest common divisor.
Calculate the GCF of 6 and 9 with method 1.
- We write down all of the divisors of each number (6 and 9), We previously explained how to find the divisors of a number.
- Identify all of the common divisors.
- Choose the greatest common divisor.
For example, the GCF of 6 and 9.
- 6: 1, 2, 3, 6,
- 9: 1, 3, 9
Their common divisors are 1 and 3.
Therefore, the GCF of 6 and 9 = 3.
Calculate the GCF of 16 and 21 with method 2.
- Factorize the numbers (16 and 21).
- We then write down the factors of each of the numbers, 16 and 21.
- See what the common factors are. In this case, as you can see, the numbers 16 and 21 do not have common factors. When two numbers do not have any common factors, the greatest common divisor is 1.
GCF of 16 and 21 = 1.
Calculate the GCF of 14, 36, and 12 with method 2.
- We decompose the numbers into prime factors.
- Then we write down the factors of each number (14, 36, and 12).
- Choose the common factors among the three numbers. In this case, the only common factor between 14, 36, and 12 is 2.
- Of the common factors, choose the one with the smallest exponent. The common factor with the smallest exponent is 2.
Therefore, the Greatest Common Divisor between 14, 36, and 12 = 2.
Continue practicing in a fun way!
If you would like to learn more topics in primary math adapted to your unique level, log in to Smartick and try it for free.
Learn More:
- How to Calculate Least Common Multiple
- Review Factoring with Examples
- Explanation of the Formula to Calculate the Least Common Multiple
- How to Simplify Fractions with Examples
- Factorization: What Is It and How Is It Done?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
The process is very easy to understand, thanks!