Is 2 A Prime Number?

Prime vs. Composite Numbers

Greetings, young math enthusiasts! Today, let’s set sail on a mathematical voyage to determine if 2 is a prime number, and learn more about the difference between prime and composite numbers.

Is 49 a Prime Number?

Or is 49 a Composite Number?

No, number 49 is not a prime number. Of course, we understand that an explanation is needed. Before we delve into the details about the number 49, let’s first cover some basics.

Is 49 a Prime Number?

Why is 49 Not a Prime Number?

What are the Prime Factors of 49?

What are the Factors of 49?

Does 49 Have 2 Factors?

Is 49 a Perfect Square?

What Type of Number is 49?

Is 49 a Semiprime Number?

Before determining if 49 is a prime number, let’s first understand the definitions of prime and composite numbers.

Prime numbers are those greater than 1, having no divisors other than 1 and themselves. In simpler terms, these numbers cannot be evenly divided by any number except for 1 and the number itself. Examples include 2, 3, 5, 7, and 11.

Composite numbers, conversely, have more than two divisors. This means they can be evenly divided by 1, the number itself, and at least one other number. For instance, 4 is composite because it can be divided by 1, 2, and 4.

Is 49 a Prime Number?

With the distinction between prime and composite numbers clear, let’s investigate if 49 is prime.

To classify 49 as a prime number, it must only be divisible by 1 and itself. Let’s examine whether this holds true.

Why is 49 Not a Prime Number?

To establish that 49 isn’t a prime number, we must check if it can be evenly divided by any number other than 1 and 49.

Dividing 49 by 1 gives 49.
Dividing 49 by 49 yields 1.

These are straightforward results. Next, let’s test other numbers:

Dividing 49 by 2 results in 24.5 (not a whole number).
Dividing 49 by 3 gives approximately 16.33 (not a whole number).
Dividing 49 by 5 results in 9.8 (not a whole number).
Dividing 49 by 7 gives 7 (a whole number).

Since 49 can be divided evenly by 7, resulting in 7, it cannot be a prime number. Thus, 49 is composite.

What are the Prime Factors of 49?

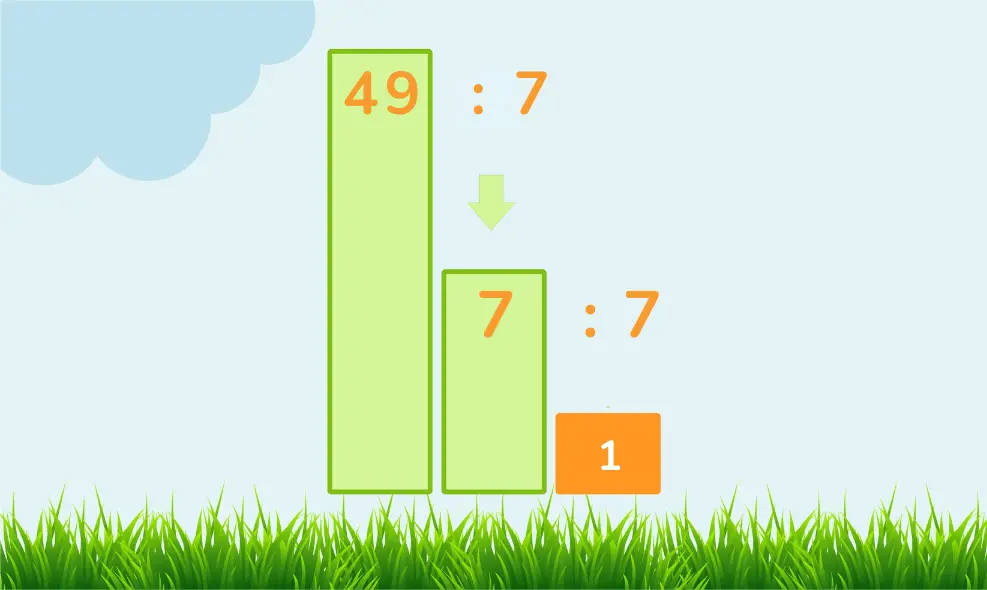
We’ve identified that 49 can be divided by 7. In fact, 49 can be expressed as:

$7 \times 7$

This indicates that the prime factor of 49 is 7, occurring twice.

What are the Factors of 49?

Factors are numbers that can be multiplied together to yield another number. For 49, the factors are:

49=7×7

Therefore, the factors of 49 are 1, 7, and 49.

Does 49 Have 2 Factors?

A prime number only has two factors: 1 and itself. Since 49 has three factors (1, 7, and 49), it does not meet the criteria for a prime number.

Is 49 a Perfect Square?

Indeed, 49 is a perfect square. A perfect square is a number that can be written as the product of an integer with itself. In this case:

$7 \times 7$

Because 7 is an integer, 49 qualifies as a perfect square.

What Type of Number is 49?

Let’s classify 49 within various mathematical categories:

Composite Number: As previously established, 49 is not prime because it has more than two divisors.
Perfect Square: 49 is a perfect square as it equals 7 times 7.
Odd Number: 49 is an odd number since it is not divisible by 2.
Natural Number: 49 is a natural number, meaning it is a positive integer.
Whole Number: 49 is a whole number, which includes all non-negative integers.
Binary Representation: In binary code, 49 is represented as 110001
Special Sequences: 49 appears in the Padovan sequence, which is a sequence of numbers where each term is the sum of the two preceding ones after the first two terms.