LCM of 3 and 5:
Exploring the Different Methods
Greetings, fellow math wayfarers! Today, we set forth on a captivating expedition into the realm of LCM, aiming to decipher the magical connection between the numbers 3 and 5. Brace yourselves for an odyssey filled with inquisitiveness and the marvels of mathematics!

LCM of 3 and 5:
Exploring the Different Methods
Greetings, fellow math wayfarers! Today, we set forth on a captivating expedition into the realm of LCM, aiming to decipher the magical connection between the numbers 3 and 5. Brace yourselves for an odyssey filled with inquisitiveness and the marvels of mathematics!


No credit card required

No credit card required
LCM of 3 and 5
Methods for Finding LCM
Prime Factorization Method
Division Method
Listing the Multiples
What is LCM of 3 and 5?
The LCM of 3 and 5 is 15! Grasping the LCM not only unravels intricate math puzzles but also adds a touch of magic to the world of fractions. Let’s delve into three captivating methods to reveal this numerical wonder!
How to Find LCM of 3 and 5?
Before we plunge into the depths of discovering the Least Common Multiple (LCM) of 3 and 5, let’s acquaint ourselves with the ingenious methods at our disposal. It’s akin to having three unique tools for a special mathematical quest. Here they are:
- Prime Factorization Method: We’ll find secret numbers that help us figure out the LCM.
- Division Method: It’s like going on a journey of dividing numbers until we get to the LCM.
- Listing the Multiples: We’ll list out the friends of 3 and 5 until we find the one they both like – that’s our LCM.
Now, let’s use these tools to solve the mystery of the LCM for 3 and 5. Ready? Let’s go!
1. Prime Factorization Method
Let’s treat numbers as astute detectives and dissect 3 and 5 into their prime agents:
- 3 = 3
- 5 = 5
Now, combine these agents to discover the LCM magic: LCM(3, 5) = 3 x 5 = 15
2. Division Method
Picture an adventurous journey of division! Divide 3 and 5 by their prime agents until we reach an impasse:
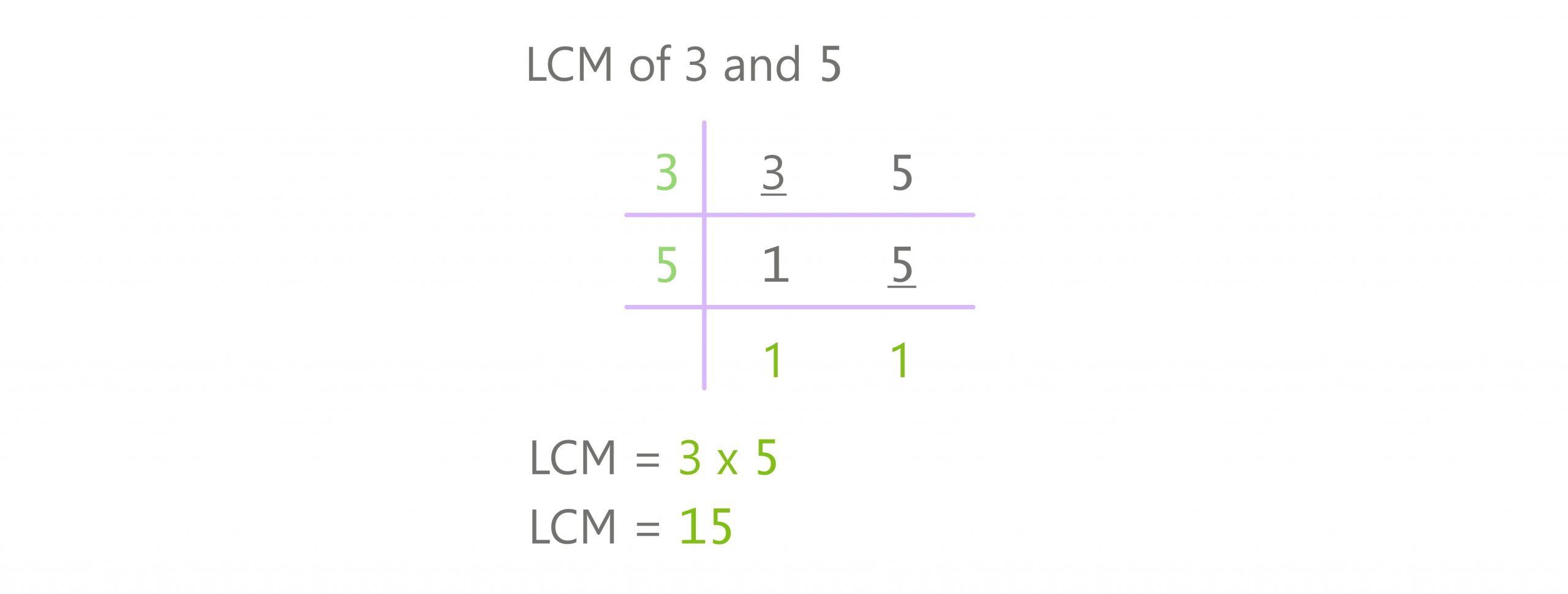
Multiply those divisors: LCM (3, 5) = 3 x 5 = 15
3. Listing Method
Unleash the potency of a 100 square to unveil the Least Common Multiple (LCM) of 3 and 5. Follow these steps for an engaging exploration:
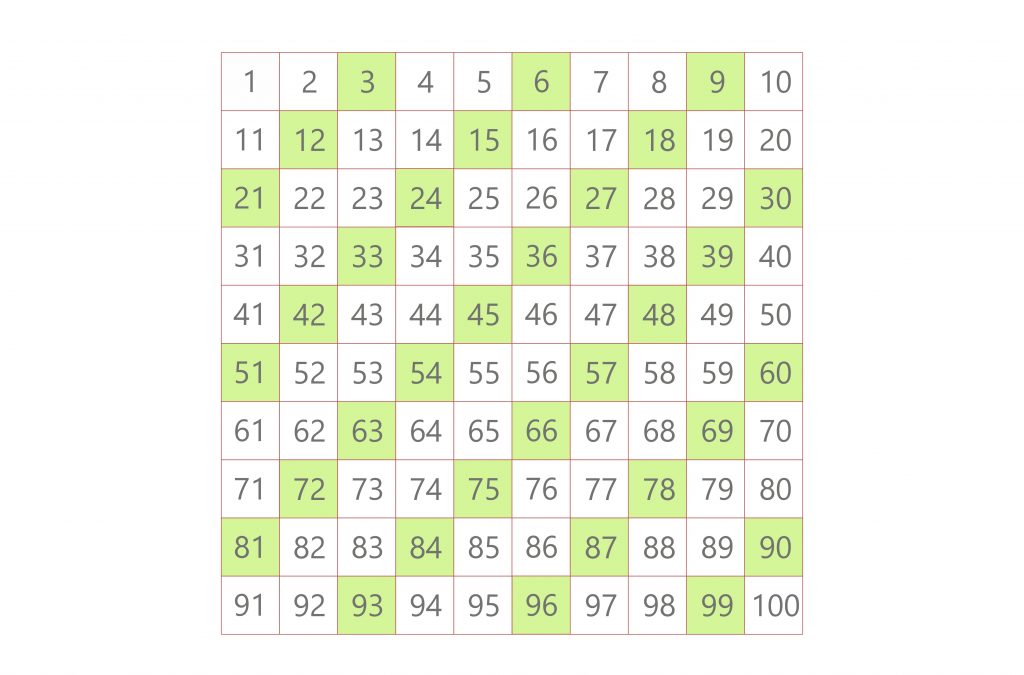
1. Identify multiples of the first number (3)
Multiples of 3: 3, 6, 9, 12, 15, 18, …
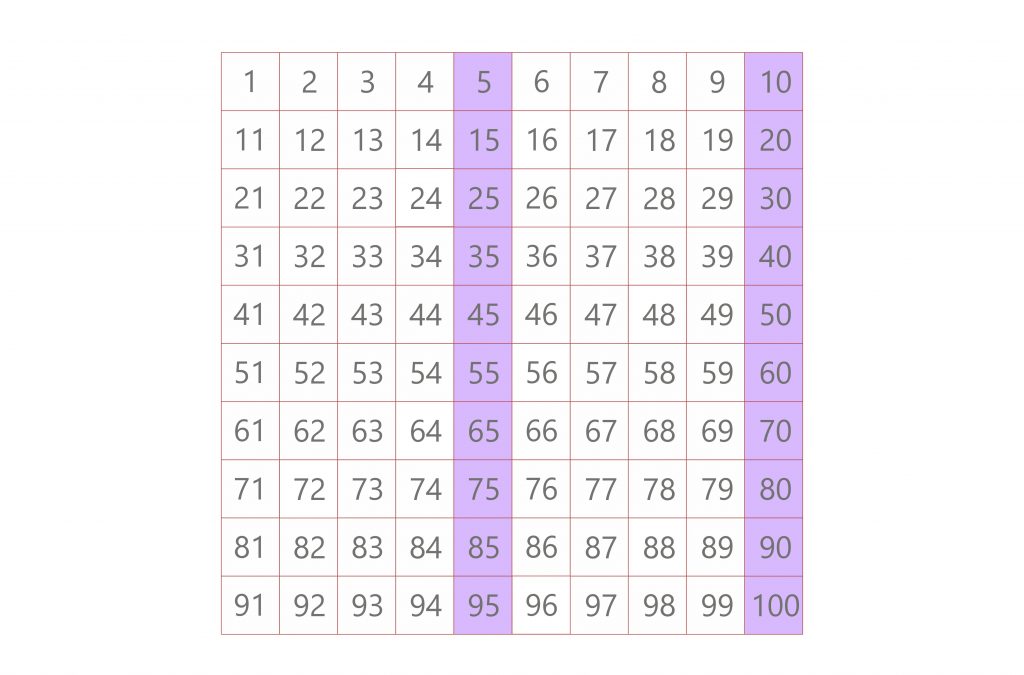
2. Identify multiples of the second number (5)
Multiples of 5: 5, 10, 15, 20, 25, 30, …
3. Find the smallest common multiple
Seek numbers that appear in both lists. In this case, 15 is the smallest number that is a multiple of both 3 and 5.
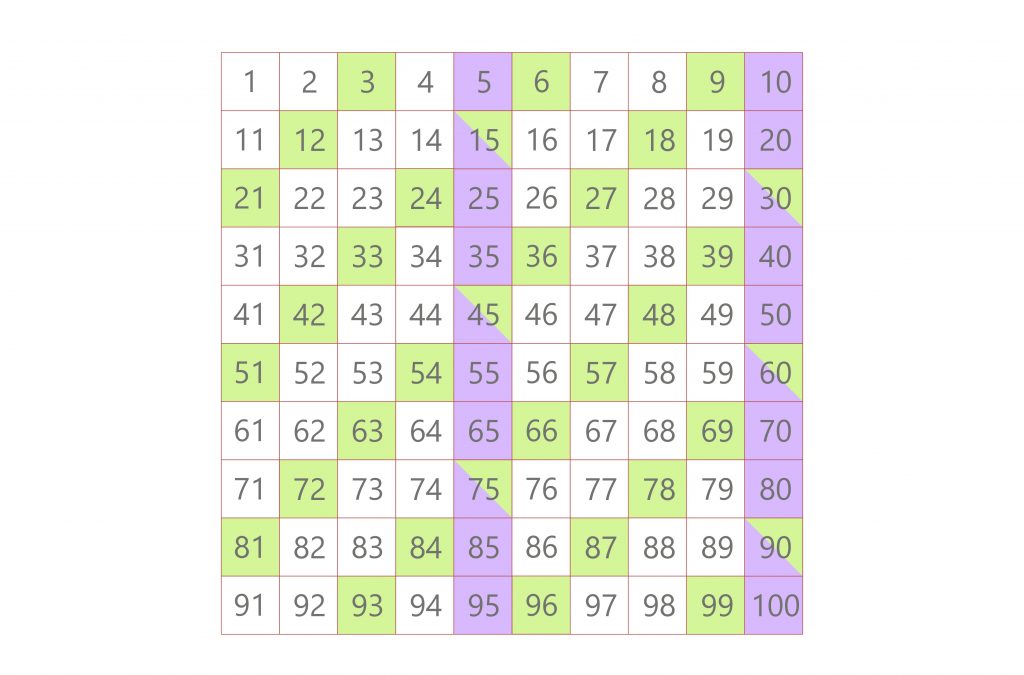
Therefore, the LCM of 3 and 5 is 15.
And there you have it, aspiring math voyagers! Unveiling the LCM of 3 and 5 is akin to unraveling the intricate dance of numerical synchrony. Keep exploring, keep smiling, and savor the enchanting world of math!
Learn More About Prime Numbers
© 2024 Smartick. All Rights Reserved.
