LCM of 2 and 6:
Exploring the Different Methods
Greetings, young math enthusiasts! Today, let’s set sail on a mathematical voyage to uncover the fascinating connection between the numbers 2 and 6. Get ready for an adventure into the captivating world of numerical wonders!

LCM of 2 and 6:
Exploring the Different Methods
Greetings, young math enthusiasts! Today, let’s set sail on a mathematical voyage to uncover the fascinating connection between the numbers 2 and 6. Get ready for an adventure into the captivating world of numerical wonders!


No credit card required

No credit card required
LCM of 2 and 6
Methods for Finding LCM
Prime Factorization Method
Division Method
Listing the Multiples
What is LCM of 2 and 6?
The LCM of 2 and 6 is 6. Understanding the LCM is like discovering a mathematical treasure chest, simplifying complex problems and making fractions a breeze. Join us as we explore three captivating methods to unveil this enchanting number!
How to Find LCM of 2 and 6?
Before we dive into our quest to find the Least Common Multiple (LCM) of 2 and 6, let’s acquaint ourselves with the magical methods at our disposal. Imagine these methods as keys to unlock the secrets of a special mission. Here they are:
- Prime Factorization Method: Unveiling the secret numbers that guide us to the LCM.
- Division Method: Embarking on a journey of division until the LCM is discovered.
- Listing the Multiples: Inviting the friends of 2 and 6 to a gathering until we find their common liking – the LCM.
Now, let’s apply these tools to unravel the LCM for 2 and 6. Are you ready? Let the mathematical journey begin!
1. Prime Factorization Method
Visualize numbers as detectives, and let’s dissect 2 and 6 into their prime agents:
- 2 = 2 x 1
- 6 = 2 x 3
Now, combine these agents to reveal the LCM magic: LCM(2,6) = 2 x 3 = 6.
2. Division Method
Embark on a division adventure! Divide 2 and 6 by their prime agents until you reach the summit:
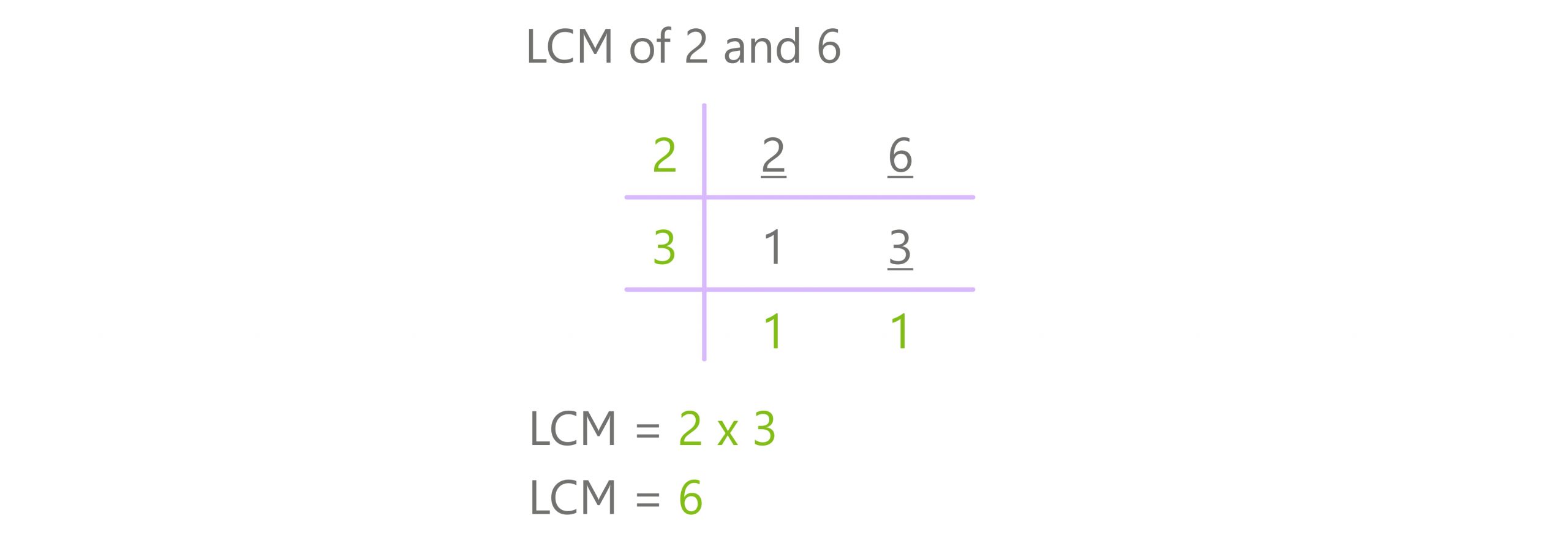
Multiply those friendly divisors: LCM (2,6) = 2 x 3 = 6.
3. Listing Method
Unleash the power of a 100 square to find the Least Common Multiple (LCM) of 2 and 6. Follow these steps for an engaging exploration:
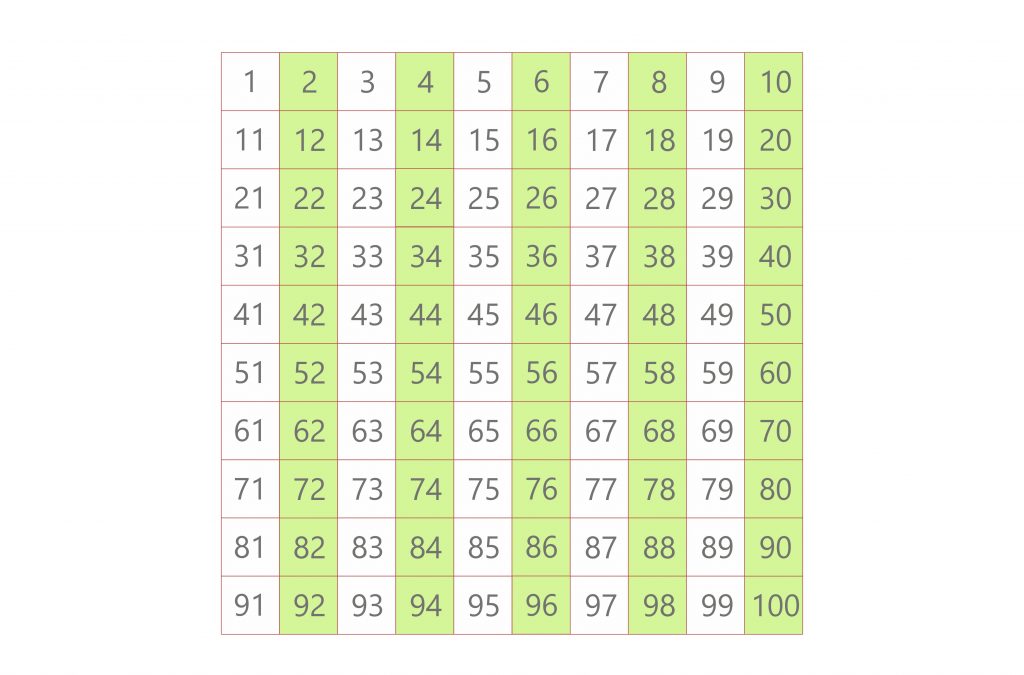
1. Identify multiples of the first number (2)
Multiples of 2: 2, 4, 6, 8, 10, …
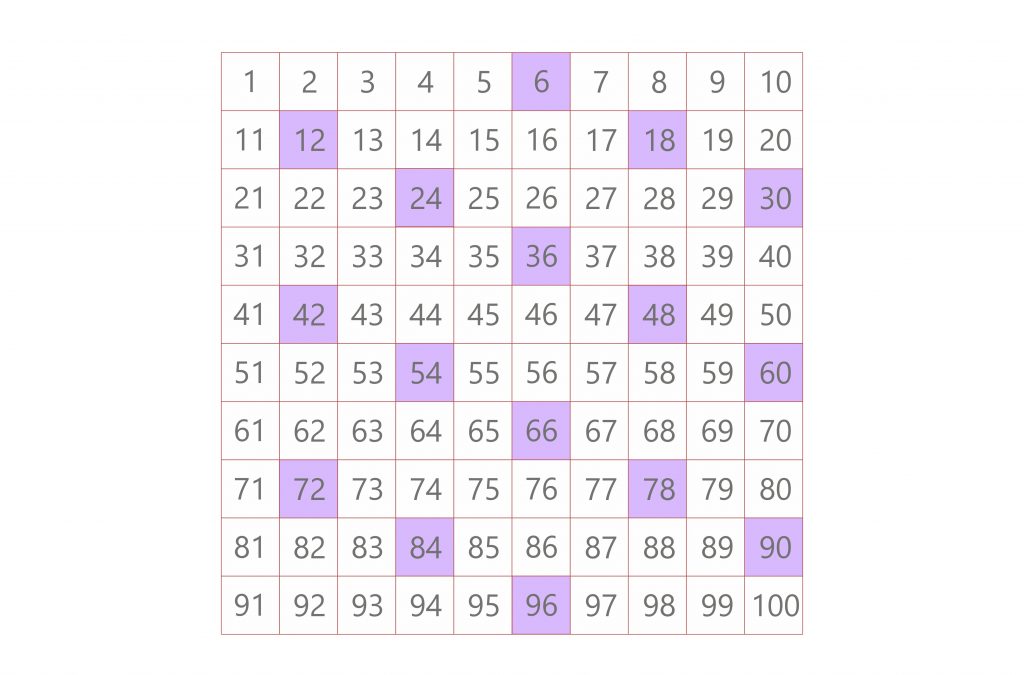
2. Identify multiples of the second number (6)
Multiples of 6: 6, 12, 18, 24, 30, …
3. Find the smallest common multiple
Look for numbers that appear in both lists. In this case, 6 is the smallest number that is a multiple of both 2 and 6.
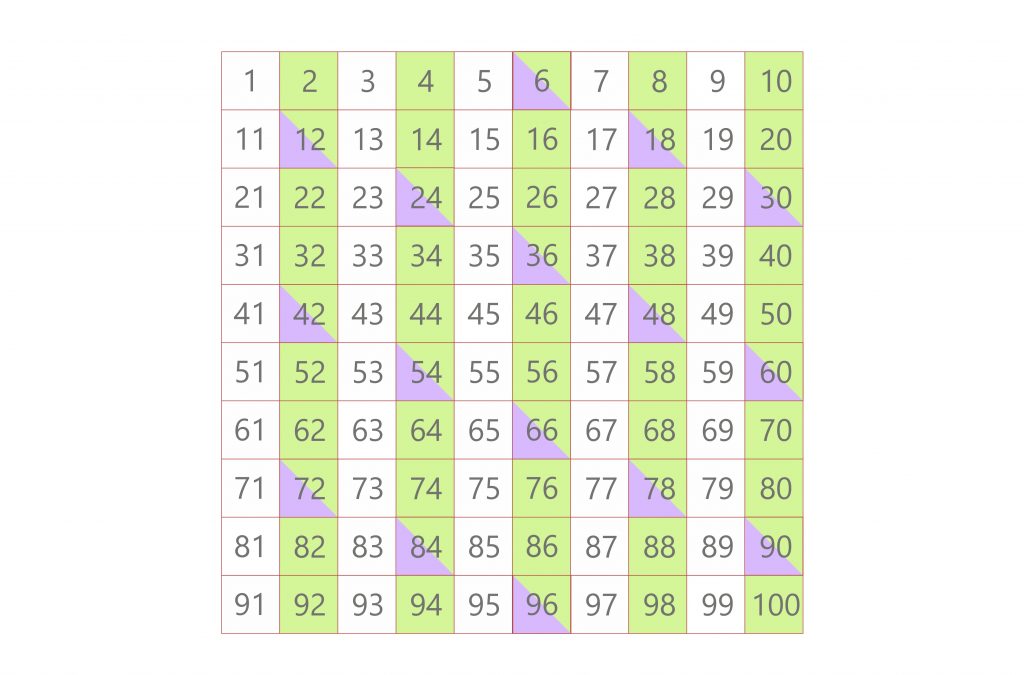
Therefore, the LCM of 2 and 6 is 6.
Congratulations, intrepid mathematicians! Navigating the numeric pathways to uncover the LCM of 2 and 6 is like embarking on a grand adventure where numbers harmonize perfectly. Keep exploring, keep smiling, and revel in the enchanting world of math!
Learn More About Prime Numbers
© 2024 Smartick. All Rights Reserved.
