Is 2 A Prime Number?
Prime vs. Composite Numbers
Greetings, young math enthusiasts! Today, let’s set sail on a mathematical voyage to determine if 2 is a prime number, and learn more about the difference between prime and composite numbers.

Is 51 a Prime Number?
Or is 51 a Composite Number?
Nope, number 51 isn’t a prime number. Curious about why? Buckle up, because we’re about to dive into the fascinating world of 51. But first, let’s lay down some groundwork to understand what makes a number prime or composite.


No credit card required

No credit card required
Is 51 a Prime Number?
Why is 51 Not a Prime Number?
What are the Prime Factors of 51?
What are the Factors of 51?
Does 51 Have 2 Factors?
Is 51 a Perfect Square?
What Type of Number is 51?
Is 51 a Semiprime Number?
Before we determine if 51 is a prime number, let’s understand the difference between prime and composite numbers.
Prime numbers are those greater than 1 that are divisible only by 1 and themselves. This means they cannot be divided evenly by any other number. Examples of prime numbers include 2, 3, 5, 7, and 11.
Composite numbers are numbers that have more than two divisors. This means they can be divided evenly by 1, the number itself, and at least one other number. For example, 4 is a composite number because it can be divided by 1, 2, and 4.
Is 51 a Prime Number?
To determine whether 51 is a prime number, we need to check if it can be divided evenly by any number other than 1 and 51.
Why is 51 Not a Prime Number?
Let’s check if 51 can be divided evenly by any numbers other than 1 and 51:
- Dividing 51 by 1 gives 51.
- Dividing 51 by 51 gives 1.
These divisions are straightforward. Now, let’s try other numbers:
- 51 divided by 2 is 25.5 (not a whole number).
- 51 divided by 3 is 17 (a whole number).
Since 51 can be divided evenly by 3 (resulting in 17), it is not a prime number. Thus, 51 is a composite number.
What are the Prime Factors of 51?
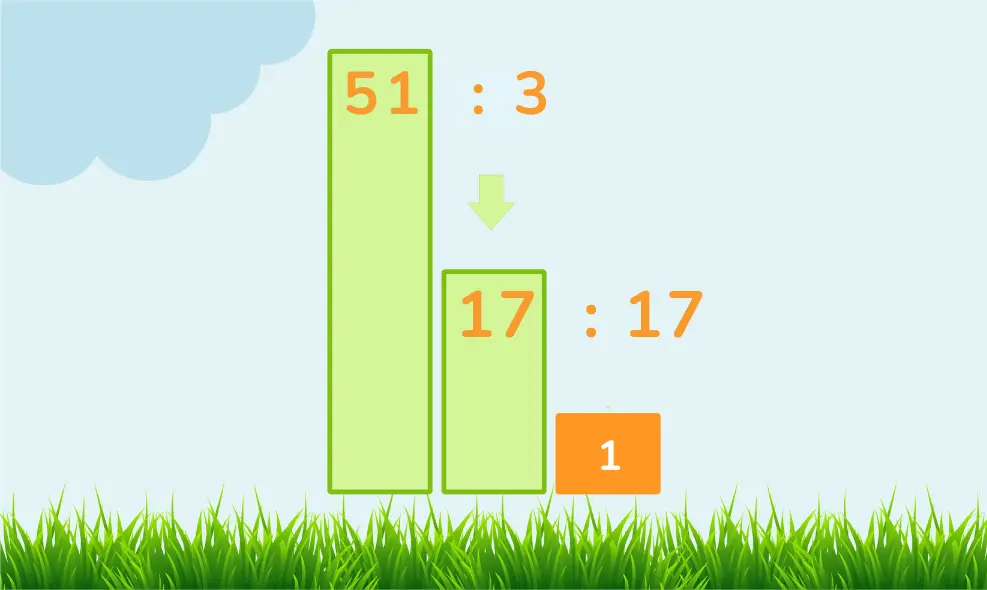
We have determined that 51 can be divided by 3. In fact, 51 can be expressed as:
51=3×17
This means the prime factors of 51 are 3 and 17.
What are the Factors of 51?
Factors are numbers that you can multiply together to get another number. For 51, the factors are:
51=3×17
So, the factors of 51 are 1, 3, 17, and 51.
Does 51 Have 2 Factors?
A prime number has only two factors: 1 and itself. Since 51 has more than two factors (1, 3, 17, and 51), it is not a prime number.
Is 51 a Perfect Square?
No, 51 is not a perfect square. A perfect square is a number that can be written as the product of an integer with itself. For example, 49 is a perfect square because:
49=7×7
There is no integer that, when multiplied by itself, equals 51.
What Type of Number is 51?
Let’s classify 51 based on different mathematical categories:
- Composite Number: As we discussed, 51 is not a prime number because it has divisors other than 1 and itself.
- Odd Number: 51 is an odd number because it is not divisible by 2.
- Natural Number: 51 is a natural number, which means it is a positive integer.
- Whole Number: 51 is a whole number, meaning it is a non-negative integer (including zero).
Is 51 a Semiprime Number?
A semiprime number is a composite number that is the product of exactly two prime numbers.
51 is indeed a semiprime number because it is the product of the prime numbers 3 and 17:
51=3×17
So, 51 fits the definition of a semiprime number.
Conclusion
To summarize, 51 is not a prime number because it can be divided evenly by numbers other than 1 and itself. Its prime factors are 3 and 17, making it a composite number. Additionally, 51 is an odd number, a natural number, and a whole number.
Finally, it is also a semiprime number because it is the product of exactly two prime numbers (3 and 17). Understanding these properties helps us categorize and better understand the nature of the number 51 in various mathematical contexts.
Learn More About Prime Numbers
© 2024 Smartick. All Rights Reserved.
