What is the Least Common Multiple?
Definition, Examples, Facts
In the magical field of mathematics, we often encounter situations where we need to find a common ground between numbers. That’s where the concept of the Least Common Multiple (LCM) comes into play.
The Least Common Multiple (LCM)
Definition, Exercises & FAQs
In the magical field of mathematics, we often encounter situations with all the prime factors where we need to find a common ground between numbers. That’s where the concept of the Least Common Multiple (LCM) comes into play.

No credit card required

No credit card required
What Is The Least Common Multiple (LCM)?
How to Find The Least Common Multiple (LCM)?
Relationship Between LCM and HCF
Difference Between LCM and HCF
FAQ
What is The Least Common Multiple (LCM)?
The Least Common Multiple (LCM) is the smallest or least common multiple that two or more numbers have in common.
Finding the LCM helps us determine a common reference point for the given numbers together, making it easier to perform operations and solve problems involving multiple quantities.
How to Find The Least Common Multiple (LCM)?
Finding the Least Common Multiple, or LCM, is like looking for a special number that can play nicely with a group of other numbers. We seek to find the least common multiple (LCM)— the smallest number that all your chosen numbers can divide evenly into, without leaving anything behind (like a remainder or a fraction).
But how do we find this friendly number? Here are one to six prime factor methods, to calculate the least common multiple (LCM of two numbers):
- Listing the Multiples Method: This method is about multiplying multiple integers, and writing out the most common multiples of each number and finding the first one they all share.
- Prime Factorization: Here, you break down each number into its basic building blocks (prime numbers) and use them to find the LCM.
- Using the Greatest Common Divisor (GCD): First, find the GCD of your numbers. Then, use a simple formula: LCM(a, b) = (a × b) / GCD(a, b).
- Using the Cake Method (Ladder Method): This visual method breaks numbers down step-by-step, similar to a ladder. By repeatedly dividing by prime numbers, you can find common factors and their multiples.
- Using the Division Method: Start by dividing the given numbers with prime numbers. Continue dividing until you reach a stage where all numbers become 1, then multiply the divisors for the LCM.
- Using the Venn Diagram: By breaking numbers into prime factors and placing them in intersecting circles, you can visually identify shared and unique factors, multiplying them together for the LCM.
Choose the method that makes the most sense to you, and you’ll have the tools you need to find the LCM! Let’s look at the first (and probably the easiest) method to arrive at the LCM:
1. How to Find LCM by Listing Multiples
Think of the “Listing Multiples Method” as a bit like sorting out toys or candies by type or color. To start, you choose the numbers you want to find the LCM for. As an example, let’s choose 5 and 6.
The LCM is the smallest multiple of numbers that each one can make when you multiply it. It’s like counting by the same number: if you pick 5, you’d then list the whole multiples of 5, 10, 15, 25, 35, and so on. If you also pick 6, you have 6, 12, 18, 24 and 30.

- Identify the numbers for which you want to find the LCM.
- Look for the smallest common multiple that appears in the list for all the numbers.
- Begin by listing the multiples of each number.
Solved Example On Listing The Multiples Method
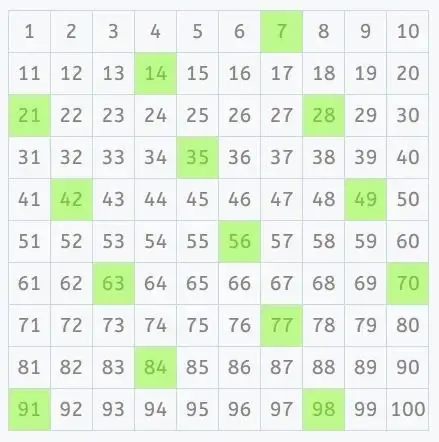
To determine the least common multiple (LCM) of two numbers using a 100 square, you can follow these steps. Let’s take the example of finding the LCM of 5 and 7:
1. Identify multiples of the first number (5)
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, …
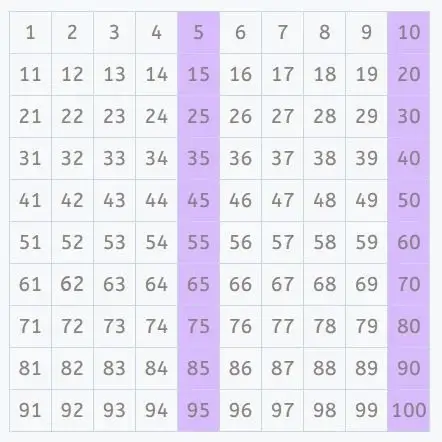
2. Identify multiples of the second number (7)
Multiples of 7: 7, 14, 21, 28, 35, 42, 49, …
3. Find the smallest common multiple
Look for numbers that appear in both lists. In this case, 35 is the smallest number that is a multiple of both 5 and 7.
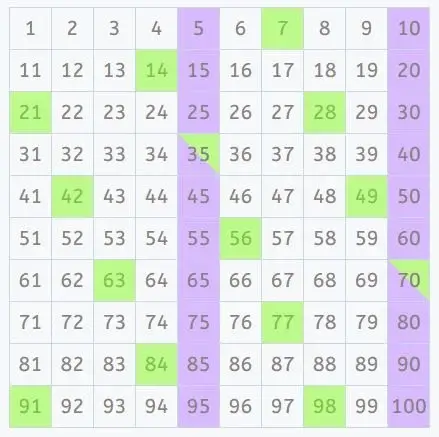
Therefore, the LCM of 5 and 7 is 35.
2. How to Find LCM by Prime Factorization
In this second method, you can imagine each number as a puzzle, and the prime factorization method is like taking each puzzle apart to see its tiniest pieces. To find the LCM using the prime factorization method, follow these steps:
- Break It Down: Start your math by breaking each number into its prime factors. It’s like seeing what tiny building blocks make up your number.
- List the Factors: Write down all the prime factors of each number. Some numbers might share some common multiples of prime factors, while others might have unique ones.
- Build Your LCM: To get the highest power of LCM, take the highest power of all the other prime numbers and factors you listed. It’s like building a new puzzle using the most pieces from each of your original prime numbers together.
3. How to Find the LCM Using the Division Method
Think of the Division Method as a step-by-step journey where you and the numbers work together. Here’s how you travel this path:
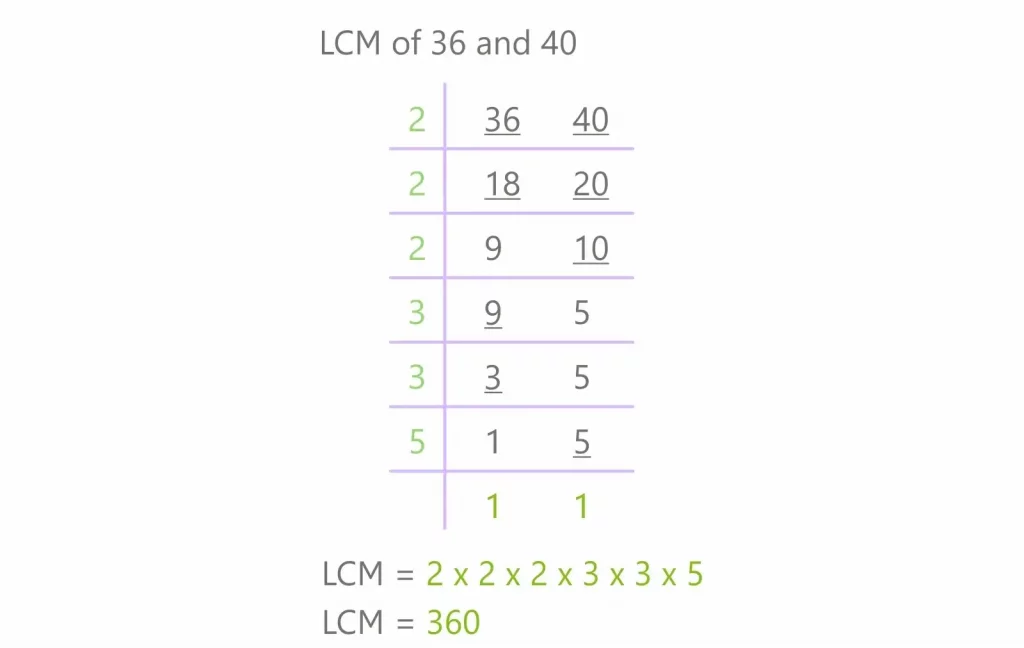
- Start Together: Place the two numbers you want to find the LCM for side by side.
- Divide by the Smallest Prime: Begin by dividing them by the smallest prime number that can divide at least one of the smaller prime numbers from below. Write the results below.
- If a number isn’t divisible by whatever of smaller prime numbers that is the smallest prime, just carry it down as is.
- Continue Dividing: Keep dividing the resulting numbers evenly divisible by prime factorization into smaller numbers. Each time, carry down any number that’s not evenly divisible by prime factorization into bigger numbers.
- Reach the End: Continue this process until you end up with all ones at the bottom.
- Multiply for the LCM: The LCM is found by multiplying all the prime numbers you have calculated and used to divide.
4. How to Find LCM Using the Cake Method (Ladder Method)
Picture the Cake Method as baking a special layered cake where each layer helps you get closer to your delicious LCM. Here’s your recipe:

- Gather Your Ingredients: Write the numbers you want to find the LCM for next to each other, like you’re setting up ingredients for baking.
- Layer by Layer: Divide these numbers by a prime number that can go into at least one of them. Write the results beneath the last row of given numbers.
- If a number isn’t divisible by that prime, simply write it down unchanged.
- Add More Layers: Continue dividing the results by prime numbers, just like you’d build up layers of a cake. Each time you divide, you’re adding another layer!
- Finish Your Cake: When all your numbers have been reduced to 1, your cake is complete.
- Taste the LCM: Multiply all the prime numbers you used to divide, and you’ll get the LCM…
- It’s the sweet result of your efforts!
The Cake (or Ladder) Method is a fun, visual way of combining numbers layer by layer, until you end up with the perfect LCM treat. Enjoy every step of the baking.
5. How to Find LCM Using the GCF Division Method
The GCF Division Method is like using a secret shortcut that both simplifies and speeds up the process of finding the LCM. Here’s your guide to this shortcut:
- Start by determining the next smallest number of Greatest Common Factor (GCF) of the two numbers you want to find the LCM for. You find the GCF by firstly stating the product of prime factors for each number, list the prime factors that are common to the two numbers, and multiply them together.
- This is the biggest number that can divide both numbers whole (without leaving a remainder).
- Use the Formula: Once you have the GCF, you can use a straightforward formula: LCM(a, b) = (a × b) / GCF(a, b). This means you’ll multiply the two numbers together and then divide by their GCF.
Results Time: The calculated result from the above calculation is your LCM.
By using the GCF Division Method, you’re leaning on the relationship between the LCM and GCF of two numbers. It’s a quicker path to the LCM, making math a bit more magical and much more efficient.
6. How to Find the LCM Using Venn Diagrams
Using Venn Diagrams to find the LCM turns math into a visual adventure. By drawing circles and filling them in, you’ll create a picture of how your numbers relate to one another.
Here’s how to sketch your way to the LCM:
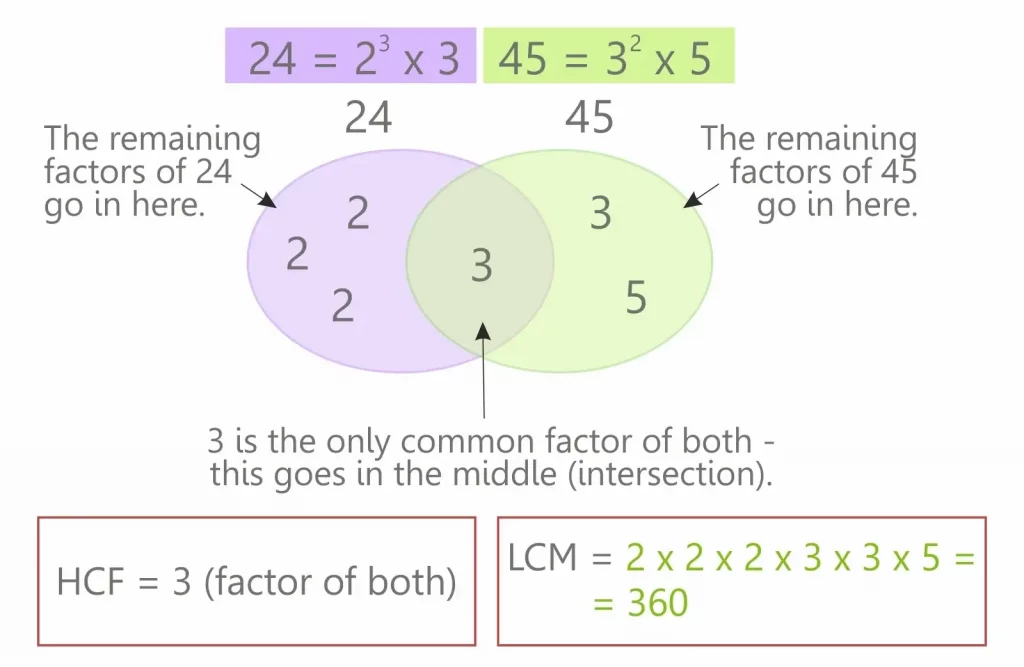
- Draw the Diagram: Start by drawing two overlapping circles for two or more numbers between numbers (add another two or more numbers between circles for additional two or more numbers, if necessary). These circles represent the prime factors of your numbers.
- Factorize and Fill: Break down each number into its own prime factorization of factors. Place the unique prime factorization of 12 first factors of the first number in its circle section, and do the same for the second number.
- For common prime factorization of factors shared by both numbers, place them in the overlapping section of the circles.
- Construct the LCM: To find the LCM, multiply all the prime factors from both circles, including whatever numbers is the smallest overlapping section. This means you’ll use all the common factors but only once.
Relationship Between LCM and GCF
LCM (Least Common Multiple) and GCF (Greatest Common Factor) are two fundamental concepts in mathematics, and they share a unique relationship.
For any two given numbers, the product of their LCM and GCF is always equal to the product of those two numbers.
In other words, for two numbers a and b: GCF (a,b) x LCM (a,b) = a x b.
This relationship illustrates how these two concepts, one focused on common multiples and the other on common factors, intertwine to connect with the inherent properties of the numbers they represent.
Understanding this link provides a deeper insight into the structure and relationship of numbers in mathematics.
Difference Between LCM and GCF
LCM (Least Common Multiple) and GCF Greatest Common Factor) are both vital mathematical concepts, but they serve distinct purposes and represent different aspects of numbers.
Here are the key differences:
- Definition: The LCM of two numbers is the smallest number that is a multiple of both, while the GCF is the largest number that can divide both numbers without leaving a remainder.
- Purpose: LCM is used to find the smallest common denominator when adding or subtracting fractions, whereas GCF helps simplify fractions to their lowest terms.
- Method: To find LCM, we look for the least number common among the multiples, while for GCF, we search for the highest number common among the factors.
- Relationship: The product of two numbers is equal to the product of their LCM and GCF.
- Application: LCM is often used in problems related to time, work, and synchronization, while GCF is applied in problems dealing with distribution, grouping, or sharing.
Understanding the difference between LCM and GCF aids in the proper application of these concepts, ensuring accurate and effective problem-solving in mathematics
Practice Exercises
Frequently Asked Questions On Least Common Multiple
Why is finding the LCM important?
Finding the LCM helps us determine a common reference point when working with multiple numbers, making calculations and comparisons more manageable.
Can the LCM of two numbers be smaller than both numbers?
No, the LCM of two numbers is always equal to or greater than the given numbers.
Is there a shortcut to find the LCM?
Yes, prime factorization is another method to find the LCM quickly. It involves breaking down each number into its prime factors and identifying the common and uncommon factors.
Can the LCM be negative?
No, the LCM is always a positive number.
Can the LCM of more than two numbers be found using the listing the multiples method?
Yes, the listing the multiples method can be applied to find the LCM of multiple numbers by considering all the given numbers together.
What are Prime Factors?
Prime factors are prime numbers that can divide another prime number without leaving a remainder. They are the basic building blocks used to express a number as a product of primes.
What is the fastest way to find the LCM?
The quickest method varies based on the numbers in question. For two smaller numbers, it’s efficient to enumerate their multiples. However, for three or more numbers, employing the prime factorization approach is advisable.
How do you find the LCM?
Find an LCM by using two integers and multiplying them. Lists the first multiple in a given number. Look at multiples in the list. If a list does not have a common multiple, write a separate common multiple on each number. See the lowest value of the two lists. These numbers are known as CLM.
What is the LCM of 6 and 8?
The LCM of 6 and 8 is 24.
What is the LCM of 8 and 12?
LCM of 8 and 12 is 24. Looking at the multiples of the two numbers, for 8 we have 8, 16, 24, 32, and for 12 we have 12, 24, 36, 48. The smallest shared number is 24. Thus, the number 24 is the “Least Common Multiple” or simply LCM.
What is the LCM of 18 and 24?
LCM of 18 and 24 is 72. By listing the multiples, for 18 they are 18, 36, 54, 72, 90, and for 24 they are 24, 48, 72, 96. The first common number is 72. Hence, 72 is referred to as the “Least Common Multiple” or LCM.
What is the LCM of 2 and 12?
LCM of 2 and 12 is 12. Observed in two-sided multiplications given numbers, the number 1 & 2 is 12, 24, 36 48. 12. The most commonly used multiples or the lowest number. 12. It has been called “Least Common Multiples” or ” Lower Common Multiples ” or LCM.
The concept of the Least Common Multiple (LCM) brings harmony to the world of numbers by finding the smallest or lowest least common multiple used, or smallest or lowest common multiple used, among them.
We have explored the definition of the LCM, learned the Listing the Least Common Multiples method to find it, and solved examples to deepen our understanding. Additionally, we addressed some frequently asked questions to clear any lingering doubts.
Now that you have unlocked the power of the LCM, embrace its magic and use it to solve a wide range of mathematical puzzles and problems.
Let the harmony of numbers guide your journey!
© 2024 Smartick. All Rights Reserved.