What is the Least Common Multiple?
Definition, Examples, Facts
In the magical field of mathematics, we often encounter situations where we need to find a common ground between numbers. That’s where the concept of the Least Common Multiple (LCM) comes into play.
Easy Way to Learn Prime Numbers:
A Complete Guide
Discover the world of prime numbers in this complete guide. Learn what prime numbers are, the definition, the small prime number, examples, charts, and easy ways to learn prime numbers effortlessly. Hop on as we sprinkle some math magic!

No credit card required

No credit card required
What are the Prime Numbers?
What Are Composite Numbers?
What are Prime Factors?
Is One a Prime Number?
What’s the Smallest Prime Number?
What’s the Smallest Odd Prime Number?
List of Prime Numbers from 1 to 100
Prime Numbers List: 100 to 1000
How to Memorize Prime Numbers?
Classes of Prime Numbers
What Are Twin Prime Numbers?
What Are Coprime Numbers?
6 Ways To Identify Prime Numbers (+ Exercises)
The History of Prime Numbers
Prime Numbers in the Real World
What are the Prime Numbers?
A prime number is a number that should have exactly two divisors: 1 and itself. In other words, it is a positive integer having exactly two factors, again, 1 and the number itself. There, the definition of prime numbers!
Take number 2 — an example of a first prime number. It can only be divided by 1 and well, 2! Right?
Three? This number is prime as well!
- 3 ÷ 3 = 1
- 3 ÷ 1 = 3
Properties of Prime Numbers
Prime numbers are much like atoms – special building blocks of which everything else is made. Like atoms, prime numbers can’t be split into smaller chunks — they are already the smallest! Meaning, they are not a product of two smaller natural numbers.
This makes them special in number theory. After all, it’s why they’re called Prime — like Optimus Prime, Prime Time, or even Amazon Prime. You see? They are quite unique.
For example, 2, 3, 5, 7, and 11 are prime numbers. If you take 7, you can’t divide it evenly by 4 or 6, can you? Every prime number is the same: you can only split it with one and itself.

Primes are important because they are the “building blocks” for other numbers. Just like LEGO bricks, you can use them to build all sorts of bigger numbers! Plus, finding prime numbers can be like a fun math treasure hunt!
What Are Composite Numbers?

Whole numbers greater than 1 that have more than two factors are called composite numbers. The remaining numbers that do not fit this definition are either prime or 1. This means they can be divided evenly by numbers other than just 1 and themselves.
These numbers are called composite numbers because they are made up of, or composed of, more than one factor (other than 1 and themselves). Knowing composite numbers will help you better understand prime numbers.
For example:
- 4: Divisible by 1, 2, and 4 (That’s one composite number!)
- 6: Divisible by 1, 2, 3, and 6 (Another one!)
- 8: Divisible by 1, 2, 4, and 8 (You got it!)
What about 13? Of course, it’s a prime! It’s divisible only by 1 and 13.
Prime and Composite Numbers are Different
Prime numbers and composite numbers are totally different. And every number — except for one special case that’s neither prime nor composite — is either one or the other. A prime or a composite!
- Prime Numbers: Can only be divided by 1 and themselves (e.g., 2, 3, 5, 7).
- Composite Numbers: Can be divided by 1, themselves, and at least one other number (e.g., 4, 6, 8).
What are Prime Factors?
Prime factors are the prime numbers that multiply together to give a particular number. Think of them as the fundamental building blocks of that number. Here’s a straightforward way to understand prime factors:
Prime Numbers are numbers greater than 1 that have no divisors other than 1 and themselves. Prime numbers include examples such as 2, 3, 5, 7, 11, and so on.
Prime Factorization is a process that finds the prime factors of a number. Simply, you divide the number by the smallest prime until you can’t divide anymore.
For example, you’d use prime numbers to factorize 18:
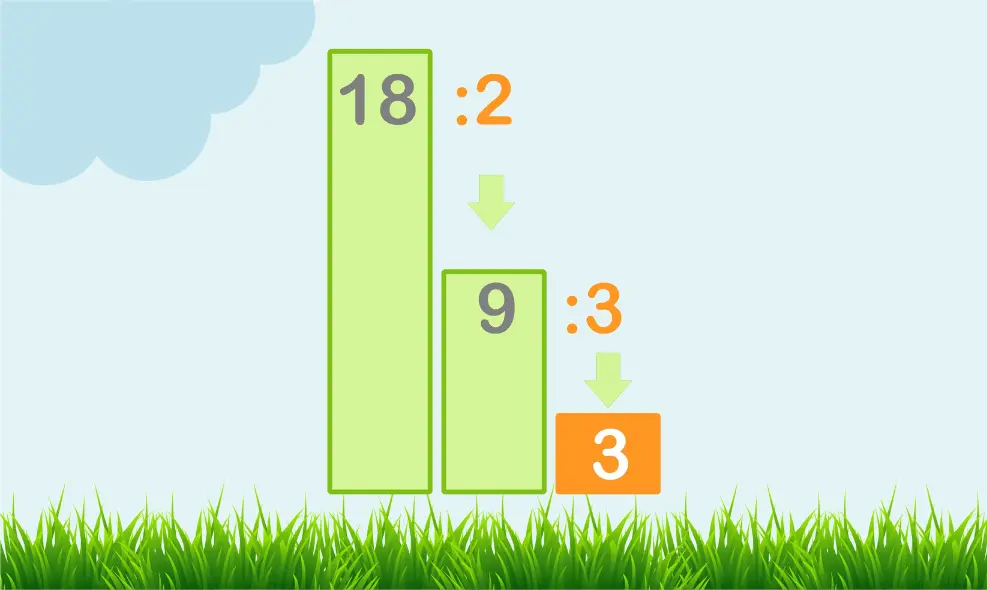
You’d start by dividing the (smallest) prime number, which is 2:
18÷2=9
So, 2 is one of the prime factors.
Now, take the result (9) and divide it by the next tiniest prime number, which is 3:
9÷3=3
There! 3 is another prime factor.
Finally, 3 is already a prime number.
Therefore, the prime factors of 18 are 2 and 3. You can write this as:
18=2×3×3 or 18=2×32
In simple terms, prime factors break down a number into the basic prime numbers that, when multiplied together, give the original number.
See? Easy peasy.
Is One a Prime Number?
No, one is not a prime number. As we said, prime numbers are numbers that are greater than 1 with exactly two factors: 1 and the given number itself. For example, 2 is a prime number because it has exactly two factors, 1 and 2.
Then what is one?
Well, it should be noted that 1 is just the first natural number and an odd number. It has no other special names. Again, 1 is neither prime nor composite. It only has one factor which is 1.
There are some properties of prime numbers that don’t apply to the number 1. Here are two examples:
Euler’s Totient Function: often written as φ(n), is a way to count the numbers less than a given number n that do not share any factors with n other than 1. Imagine you have a group of numbers from 1 up to n. Euler’s Totient Function tells you how many of these numbers can be paired with n and have no common factors (except for 1).
Sum of Divisors Function: This function, denoted as σ(n), gives the sum of all positive divisors of n. For a prime number p, the sum of divisors is 1 + p because the only divisors are 1 and the number itself. For example, σ(5) = 1 + 5 = 6. For the number 1, σ(1) = 1, because the only divisor of 1 is 1 itself.
What’s the Smallest Prime Number?
2 is the smallest prime! It’s an even number and the first natural number greater than 1 that is a prime.
One other thing… All prime numbers are odd numbers except 2. Yup, two is the only even prime number among the rockstars.
What’s the Smallest Odd Prime Number?
The smallest odd prime number is 3. After 2, it’s the next in line.
So, we have two prime numbers right at the start: 2 (the smallest and only even prime number) and 3 (the smallest odd prime number).
Here’s what’s fascinating about this dream couple: they are the only consecutive prime numbers. All others are separated by — you guessed it — composite numbers.
List of Prime Numbers from 1 to 100
There are 25 prime numbers from 1 to 100. The lowest out of 100 is the number 2 while the largest prime number in the group is 97.
Here’s the prime number chart listing all 25.
Here’s the prime numbers list in writing: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Find Prime Numbers 1 to 100! (Prime Numbers Chart)
Let’s create a table with all the prime numbers up to 100.
We start with 2. Since 2 is a prime number, all multiples of 2 will be composite. We cross out all multiples of 2 on the table.
Next, we have 3, another prime number. We cross out all multiples of 3 because they are composite.
Then, we move to the next prime number, which is 5. We cross out all multiples of 5.
Following 5, we have 7. We cross out all multiples of 7.
The next prime number is 11. We cross out all multiples of 11, which are 22, 33, 44, 55, 66, 77, 88, and 99. Oh, look! These numbers are already crossed out from previous steps.
There you go! The list of prime numbers 1 to 100. You don’t need to memorize all of them, but it helps to remember the smaller ones like 2, 3, 5, 7, 11, and 13.
Prime Numbers List: 100 to 1000
Let’s explore the prime numbers between 100 and 1,000.
While we can’t list every single one here, as there are infinitely many, we can highlight some key ones for you!
How to Memorise Prime Numbers?
Memorizing Prime Numbers from 1 to 20
Let’s start with the prime numbers from 1 to 20. Here they are:
2, 3, 5, 7, 11, 13, 17, 19
One fun way to remember these is to make a song out of them. You can use the tune of ‘Twinkle, Twinkle, Little Star.’ Here’s a quick example:
‘2, 3, 5 and 7, Primes are fun, numbers in heaven. 11, 13, 17, 19, Just composite numbers numbers in between.’
Try singing this a few times, and you’ll start to remember them!
Memorizing Prime Numbers from 1 to 100
Now, as we get more comfortable with primes, let’s look at more of them up to 100. We’ll break them down into smaller groups to make it easier.
For example, let’s focus on one group at a time:
- 2, 3, 5, 7
- 11, 13, 17, 19, 23, 29
- 31, 37, 41, 43, 47, 53
- 59, 61, 67, 71, 73, 79
- 83, 89, 97
You can make flashcards with each prime number on them and play matching games. Pair the primes and see how quickly you can find all the matches! Also, make sure you recognize patterns. For example, except for 2 and 5, all prime numbers end in 1, 3, 7, or 9.
You can also create a mnemonic story or phrase where each word starts with the same letter or a similar-sounding letter to the prime number.
Lastly, keep in mind that prime numbers are much easier to recognize than to remember. Therefore, don’t sweat yourself to much to remember these numbers. Instead, remember the division principles and factors you can devide these numbers with. It will be a whole lot easier!
Classes of Prime Numbers

Prime numbers are fascinating and come in many different classes, each with a unique name. Some of these names are quite funny, like lucky, sexy, happy, and cousin, almost as if they were named after dwarfs! Imagine a group of playful dwarfs called Lucky, Sexy, Happy, and Cousin, each with their own special traits. These playful names add a bit of fun to the serious world of mathematics.
Other prime classes carry the names of the great mathematicians who discovered them, like Fermat primes and Mersenne primes. These names pay homage to the brilliant minds who contributed to our understanding of these special numbers.
There are at least 34 different classes of prime numbers, each named for specific patterns or properties they have. Here are the classes of prime numbers:
- Balanced prime
- Chen prime
- Circular prime
- Cluster prime
- Cousin prime
- Cuban prime
- Cullen number
- Cullen prime
- Delicate prime
- Dihedral prime
- Double Mersenne prime
- Eisenstein prime
- Emirp
- Factorial prime
- Fermat number
- Fibonacci prime
- Fortunate prime
- Full reptend prime
- Gaussian prime
- Genocchi prime
- Good prime
- Happy prime
- Higgs prime
- Highly cototient prime
- Irregular prime
- Left-and-right-truncatable prime
- Left-truncatable prime
- Long prime
- Lucas prime
- Lucky prime
- Mersenne prime
- Mills prime
- Minimal prime (recreational mathematics)
- Motzkin prime
- Newman–Shanks–Williams prime
- Palindromic prime
- Pell prime
- Pell-Lucas prime
- Permutable prime
- Pierpont prime
- Pillai prime
- Prime quadruplet
- Prime triplet
- Primorial prime
- Proth prime
- Pythagorean prime
- Quartan prime
- Ramanujan prime
- Regular prime
- Repunit prime
- Right prime
- Right-truncatable prime
- Safe prime
- Sexy prime
- Solinas prime
- Sophie Germain prime
- Stern prime
- Strobogrammatic number
- Strong prime
- Super-prime
- Supersingular prime (algebraic number theory)
- Supersingular prime (moonshine theory)
- Truncatable prime
- Twin prime
- Wagstaff prime
- Wall–Sun–Sun prime
- Wieferich prime
- Williams number
- Wilson prime
- Wolstenholme prime
- Wolstenholme’s theorem
- Woodall number
- Woodall prime
What Are Twin Prime Numbers?
Twin prime numbers are pairs of prime numbers that have a difference of exactly two. Meaning there’s only one composite number between them. In other words, if p is a prime, p and p+2 are both a twin pair.
Consider them the best friends in the world of mathematics. They hang out together with just one even number between them.
Here are some examples of prime numbers residing close to one another:
- (3, 5) These two are the smallest twins.
- (11, 13)
- (17, 19) They form a prime twin as well!
- (29, 31) 1 and p (29) form a composite number, 30!.
- (41, 43)
Should 2 and 3 be Considered Twins?
No, 2 and 3 are not considered twin prime numbers. Twins are pairs of prime numbers that have only two as a difference. No exceptions! Since the prime gaps between 2 and 3 are non-existent, they do not meet this criterion.
To wrap up, a twin prime should have exactly two numbers as the difference from its twin.
What Are Coprime Numbers?
Coprime numbers share only one thing in common: the number 1! When you look at two numbers, if the only factor they both share is 1, then those numbers are called coprime.
How to check if the numbers are coprime?
List the Factors: Write down all the factors (numbers that divide evenly) of each number.
- For example, let’s look at the two different primes: 8 and 15.
- Factors of 8: 1, 2, 4, 8
- Factors of 15: 1, 3, 5, 15
Find Common Factors: See which factors are the same for both numbers.
- Common factors of 8 and 15? Just 1!
Since 1 is the only common factor, 8 and 15 are coprime.
6 Ways To Identify Prime Numbers (+ Exercises)
Here are some simple tricks to help you identify prime numbers, along with small exercises to practice each method:
1. Divisibility Rule
Prime numbers can only be divided by 1 and themselves. For a number to be prime, it should not be divisible evenly by any other number.
Exercise:
Take the number 29. Try dividing it by 2, 3, 4, and 5. If none of these divisions result in a whole number, then 29 is prime.
2. Check for Evenness
Any even number greater than 2 is not a prime number, because it is divisible by 2.
Exercise:
Is 58 a prime number? Since 58 is even and greater than 2, it is not prime.
3. The Square Root Method
For any number n, where n is a natural number, check divisibility by all prime numbers less than or equal to the square root of n. If n is not divisible by any of these primes, it is a prime number.
Exercise:
Determine if 37 is a prime number. The square root of 37 is approximately 6.1. Check divisibility by 2, 3, and 5 (primes less than 6.1). Since 37 is not divisible by any of these, it is prime.
4. The Sieve of Eratosthenes
This ancient method helps identify all prime numbers up to a certain limit. Write down all numbers up to your limit, and repeatedly mark the multiples of each prime number starting from 2.
Want a fun fact? You already tried the sieve of Eratosthenes!
Here’s the exercise to remind you:
Find all prime numbers up to 30:
- List numbers from 2 to 30.
- Cross out all multiples of 2, 3, 5, and 7.
- The remaining numbers are primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
5. Prime Number Patterns
Remember that except for 2 and 3, all primes are of the form 6k±16k (where k is a whole number). This is because any number of the form 6k, 6k+2, 6k+3, or 6k+4 is divisible by 2 or 3.
Exercise:
Check if 89 is a prime number.
- 89÷6 ≈14.83
- The nearest multiples of 6 are 84 (6×14) and 90 (6×15).
- Check 89 – 84 = 5 and 90 – 89 = 1, confirming that 89 fits the form 6k−1, and isn’t divisible by 2 or 3.
6. Using Prime Factorization
For this one, you’ll use primes or prime factorizations. Try breaking down a number into its prime factors. Of course, if you end up with only the number itself and 1, then it’s prime.
Exercise:
Is 51 a prime number?
- Try dividing 51 by 2, 3, 5, and 7.
- 51÷3=1751 \div 3 = 1751÷3=17
- Since 17 is also a prime number, 51 has factors other than 1 and itself, so it is not prime.
By practicing these tricks and exercises, you can become more comfortable identifying prime numbers.
The History of Prime Numbers
Prime numbers have a rich history that dates back to ancient times. The Egyptian number theorists, around 1550 BC, worked with prime numbers in their math texts. The Greeks, particularly Euclid, made significant contributions around 300 BC. His contribution is the sole reason the entire theorem is named after him — that’s right, Euclid’s Theorem.
Some 1300 years later, in the Islamic Golden Age around 1000 AD, mathematician Ibn al-Haytham made further discoveries. He found Wilson’s theorem — only, the thing was nameless back then. Around 700 years later, Edward Waring announced the theorem and named it “Wilson’s” to show his gratitude to John Wilson, his student.
By the 17th century, Pierre de Fermat formulated Fermat’s Little Theorem and investigated new Fermat primes, which was later proved by Leibniz and Euler. Fermat and Mersenne studied specific types of primes, such as Fermat primes and Mersenne primes. Euler also proved that all even perfect numbers are linked to Mersenne primes.
In the 19th century, mathematicians like Legendre and Gauss developed another one — the prime number theorem. It describes the distribution of primes. This theorem was proven by Hadamard and de la Vallée Poussin in 1896. Later, Dirichlet showed that certain arithmetic progressions contain infinitely many primes.
With the advent of computers, finding huge prime numbers became more feasible. The largest known primes have been discovered using computer algorithms since 1951.
What is The Largest Known Prime Number?
The largest known prime number is 282,589,933−1. This enormous number has 24,862,048 digits and was discovered on December 7, 2018, by Patrick Laroche, a volunteer for the Great Internet Mersenne Prime Search (GIMPS).
This prime number is special because it is a Mersenne prime. Mersenne prime number can be expressed in the form 2p−1, where p is also a prime number. In this case, p is 82,589,933. Laroche’s computer ran for 12 days non-stop to verify this prime. Other computers confirmed it using different methods to ensure accuracy.
Finding large complex numbers helps scientists and mathematicians understand more about numbers and can even be used in technology, like cryptography, to keep information safe online. It’s an exciting part of math where anyone can contribute and discover something new.
What is Euclid’s Theorem?
Euclid’s Theorem states that there are infinitely many prime numbers. In simple terms, it means that no matter how many large prime numbers you find, there will always be more out there.
Although 282,589,933−1 remains prime biggest in size, in theory, prime numbers are infinite.
Meaning, you can never run out of prime numbers because they go on forever. This idea was first proven by the ancient Greek mathematician Euclid over 2,000 years ago. His proof is still considered one of the most elegant in mathematics.
Euclid proved this by showing that if you take all known prime numbers and multiply them together, then add 1, the result will either be a new prime number or prime factors that are not in your original list. This means you can always find a new number that is prime, proving that the list is endless.
What is a Prime Number Theorem
The Prime Number Theorem is a fundamental result in number theory that describes how prime numbers are distributed among the positive integers. Here’s a simple explanation:
Imagine you have a very long number line with all the positive integers. Primes are like rare gems scattered along this line. The Prime Number Theorem helps us understand how these gems are distributed as you move further and further along the number line.
Prime Numbers in the Real World
Prime numbers might seem like simple, isolated digits, but they’re incredibly useful!
Software engineers rely on these numbers for cyber security. Keeping information secure is crucial in today’s digital world. Engineers use encryption to protect sensitive data like credit card details and personal messages.
Here’s how it works: prime numbers are used by cyber security experts who choose two extremely large prime numbers (some with over a hundred digits) and multiply them together to create an even larger number. This large number is used to encrypt data, making it secure.
If a hacker tries to access this data, they must figure out the two original prime factors. Because these prime numbers are so large, it could take hackers years or even decades to solve the puzzle. Good luck with that! Prime numbers are the numbers that keep our personal information online safe and secure!
© 2024 Smartick. All Rights Reserved.


